Rotor Machines

ROTOR MACHINES

The example just given suggests that multiple stages of encryption can produce an algorithm that is significantly more difficult to cryptanalyze. This is as true of substi-tution ciphers as it is of transposition ciphers. Before the introduction of DES, the most important application of the principle of multiple stages of encryption was a class of systems known as rotor machines.9

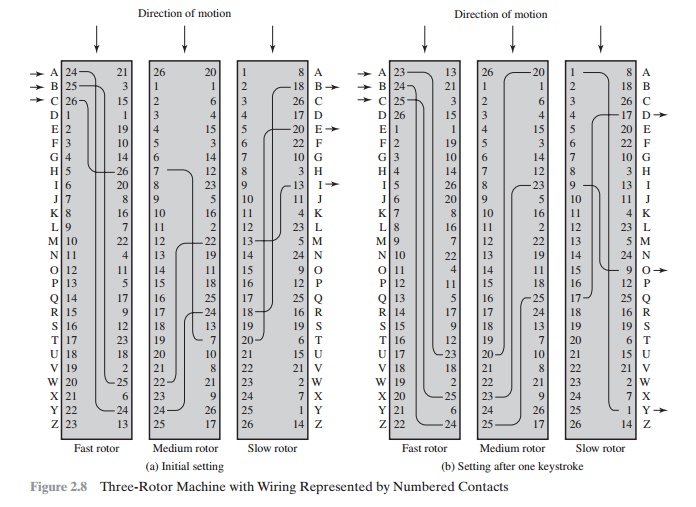
The basic principle of the rotor machine is illustrated in Figure 2.8. The machine consists of a set of independently rotating cylinders through which electri-cal pulses can flow. Each cylinder has 26 input pins and 26 output pins, with internal wiring that connects each input pin to a unique output pin. For simplicity, only three of the internal connections in each cylinder are shown.

If we associate each input and output pin with a letter of the alphabet, then a single cylinder defines a monoalphabetic substitution. For example, in Figure 2.8, if an operator depresses the key for the letter A, an electric signal is applied to the first pin of the first cylinder and flows through the internal connection to the twenty-fifth output pin.

Consider a machine with a single cylinder. After each input key is depressed, the cylinder rotates one position, so that the internal connections are shifted accordingly. Thus, a different monoalphabetic substitution cipher is defined. After 26 letters of plaintext, the cylinder would be back to the initial position. Thus, we have a poly-alphabetic substitution algorithm with a period of 26.

A single-cylinder system is trivial and does not present a formidable cryptana-lytic task. The power of the rotor machine is in the use of multiple cylinders, in which the output pins of one cylinder are connected to the input pins of the next. Figure 2.8 shows a three-cylinder system. The left half of the figure shows a position in which the input from the operator to the first pin (plaintext letter a) is routed through the three cylinders to appear at the output of the second pin (ciphertext letter B).

With multiple cylinders, the one closest to the operator input rotates one pin position with each keystroke. The right half of Figure 2.8 shows the system’s config-uration after a single keystroke. For every complete rotation of the inner cylinder, the middle cylinder rotates one pin position. Finally, for every complete rotation of the middle cylinder, the outer cylinder rotates one pin position. This is the same type of operation seen with an odometer. The result is that there are 26 * 26 * 26 = 17,576 different substitution alphabets used before the system repeats. The addition of fourth and fifth rotors results in periods of 456,976 and 11,881,376 letters, respectively. As David Kahn eloquently put it, referring to a five-rotor machine [KAHN96, ]:

A period of that length thwarts any practical possibility of a straightforward solution on the basis of letter frequency. This general solution would need about 50 letters per cipher alphabet, meaning that all five rotors would have to go through their com-bined cycle 50 times. The ciphertext would have to be as long as all the speeches made on the floor of the Senate and the House of Representatives in three successive sessions of Congress. No cryptanalyst is likely to bag that kind of trophy in his lifetime; even diplomats, who can be as verbose as politicians, rarely scale those heights of loquacity.

The significance of the rotor machine today is that it points the way to the most widely used cipher ever: the Data Encryption Standard (DES). This we examine in Chapter 3.