Speed Control of DC Shunt Motor: Varying Armature Resistance, Field Resistance

Speed Control Of Dc Shunt Motor

We know that the speed of shunt motor is given by:

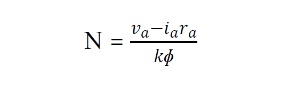
Where,Va is the voltage applied across the armature,

N is the rotor speed and φ is the flux perpole and is proportional to the field current If. As explained earlier, armature current Ia is decided by the mechanical load present on the shaft. Therefore, by varying Va and If we canvary n. For fixed supply voltage and the motor connected as shunt we can vary Vabycontrolling an external resistance connected in series with the armature. If of course can bevaried by controlling external field resistance Rfconnected with the field circuit. Thus for.shunt motor we have essentially two methods for controlling speed, namely by:

1.                                              Varying Armature Resistance

2.                                              Varying Field Resistance

1. Speed Control by Varying Armature Resistance

The inherent armature resistance Ra being small, speed n versus armature current (Ia) characteristic will be a straight line with a small negative slope as shown in figure.

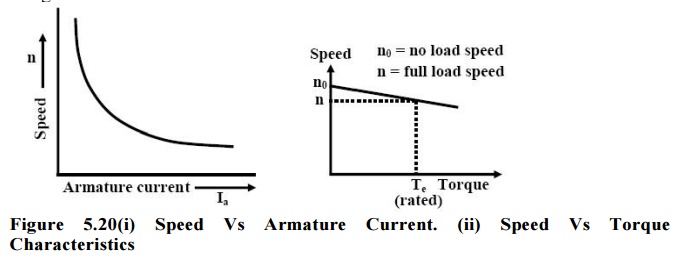
Note that for shunt motor voltage applied to the field and armature circuit are same and equal to the supply voltage V. However, as the motor is loaded, IaRa drop increases making speed a little less than the no load speed n0. For a well designed shunt motor this drop in speed is small and about 3 to 5% with respect to no load speed. This drop in speed from no load to full load condition expressed as a percentage of no load speed is called the inherent speed regulation of the motor. It is for this reason, a d.c shunt motor is said to be practically a constant speed motor since speed drops by a small amount from no load to full load condition.

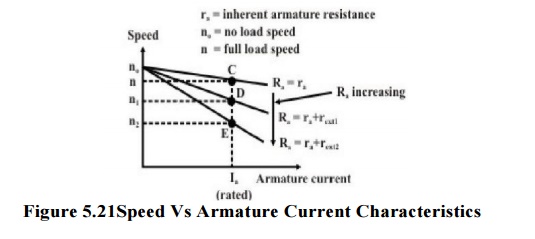
From these characteristic it can be explained how speed control is achieved. Let us assume that the load torque TL is constant and field current is also kept constant. Therefore, since steady state operation demands Te = TL, Te= kφ too will remain constant; which meansIa will not change. Suppose Rest = 0, then at rated load torque, operating point will be at C andmotor speed will be n. If additional resistance rext1 is introduced in the armature circuit, newsteady state operating speed will be n1 corresponding to the operating point D.

This same load torque is supplied at various speed. Variation of the speed is smooth and speed will decrease smoothly if Rest is increased. Obviously, this method is suitable for controlling speed below the base speed and for supplying constant rated load torque which ensures rated armature current always. Although, this method provides smooth wide range speed control (from base speed down to zero speed), has a serious draw back since energy loss takes place in the external resistance Rest reducing the efficiency of the motor.

2. Speed Control by Varying Field Current

In this method field circuit resistance is varied to control the speed of a d.c shunt motor. Let us rewrite .the basic equation to understand the method.

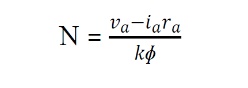
If we vary If , flux φ will change, hence speed will vary. To change If an external resistance is connected in series with the field windings. The field coil produces rated flux when no external resistance is connected and rated voltage is applied across field coil. It should be understood that we can only decrease flux from its rated value by adding external resistance. Thus the speed of the motor will rise as we decrease the field current and speed control above the base speed will be achieved. Speed versus armature current characteristic is shown in figure for two flux valu es φ and φ1. Since φ1<φ, the no load speed no' for flux value φ1 is more than the no load speed no corresponding to φ.

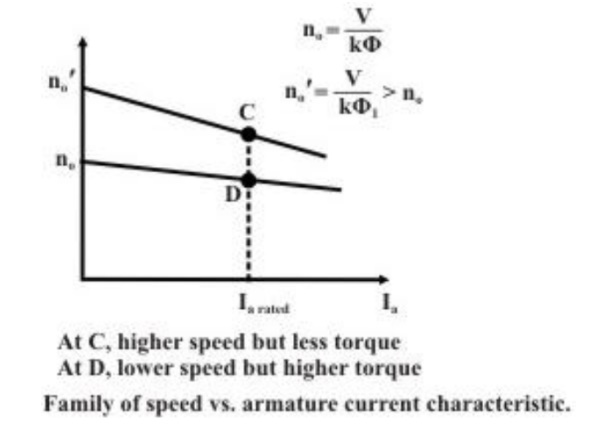
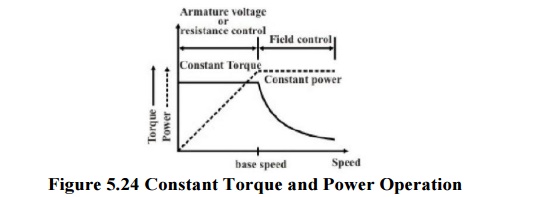
However, this method will not be suitable for constant load torque .To make this point clear, let us assume that the load torque is constant at rated value. So from the initial steady condition, we have TL rated=Ta1= k=Ia rated .If load torque remains constant and flux is reduced to φ1, new armature current in the steady state is obtained from kI a1=TL rated . Therefore new armature current is but this fraction is less than 1. Hence new armature current will be greater than the rated armature current and the motor will be overloaded. This method therefore, will be suitable for a load whose torque demand decreases with the rise in speed keeping the output power constant as shown in figure. Obviously this method is based on flux weakening of the main field.