Chapter: Electrical machines : DC Motor
Braking of DC shunt motor
Braking of D.C shunt motor:
basic idea
It is often necessary in many applications to stop a running motor rather quickly. We know that any moving or rotating object acquires kinetic energy. Therefore, how fast we can bring the object to rest will depend essentially upon how quickly we can extract its kinetic energy and make arrangement to dissipate that energy somewhere else. If you stop pedaling your bicycle, it will eventually come to a stop eventually after moving quite some distance. The initial kinetic energy stored, in this case dissipates as heat in the friction of the road. However, to make the stopping faster, brake is applied with the help of rubber brake shoes on the rim of the wheels. Thus stored K.E now gets two ways of getting dissipated, one at the wheel-brake shoe interface (where most of the energy is dissipated) and the other at the road-tier interface. This is a good method no doubt, but regular maintenance of brake shoes due to wear and tear is necessary.
If a motor is simply disconnected from supply it will eventually come to stop no doubt, but will take longer time particularly for large motors having high rotational inertia. Because here the stored energy has to dissipate mainly through bearing friction and wind friction. The situation can be improved, by forcing the motor to operate as a generator during braking. The idea can be understood remembering that in motor mode electromagnetic torque acts along the direction of rotation while in generator the electromagnetic torque acts in the opposite direction of rotation. Thus by forcing the machine to operate as generator during the braking period, a torque opposite to the direction of rotation will be imposed on the shaft, thereby helping the machine to come to stop quickly. During braking action, the initial K.E stored in the rotor is either dissipated in an external resistance or fed back to the supply or both.
1. Rheostatic braking
Consider a d.c shunt motor operating from a d.c supply with the switch S connected to position 1 as shown in figure 39.23. S is asingle pole double throw switch and can be connected either to position 1 or to position 2. One end of an external resistance Rb is connected to position 2 of the switch S as shown.
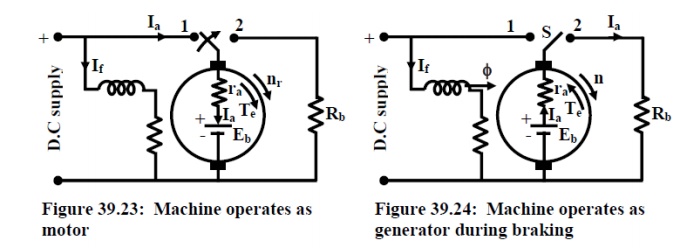
Let with S in position 1, motor runs at n rpm, drawing an armature current Ia and the back emf is Eb = kŽå n. Note the polarity of Ebwhich, as usual for motor mode in opposition with the supply voltage. Also note Te and n have same clock wise direction.
Now if S is suddenly thrown to position 2 at t = 0, the armature gets disconnected from the supply and terminated by Rb with field coil remains energized from the supply.
Since speed of the rotor can not change instantaneously, the back emf value Eb is still maintained with same polarity prevailing at t = 0-. Thus at t = 0+, armature current will be Ia = Eb/(ra + Rb) and with reversed direction compared to direction prevailing during motor mode at t = 0.
Obviously for t > 0, the machine is operating as generator dissipating power to Rb and now the electromagnetic torque Te must act in the opposite direction to that of n since Ia has changed direction but Žå has not (recall Te ŌłØ Žå Ia). As time passes after switching, ndecreases reducing K.E and as a consequence both Eb and Ia decrease. In other words value of braking torque will be highest at t = 0+, and it decreases progressively and becoming zero when the machine finally come to a stop.
2. Plugging or dynamic braking
This method of braking can be understood by referring to figures 39.25 and 39.26. Here S is a double pole double throw switch. For usual motoring mode, S is connected to positions 1 and 1'. Across terminals 2 and 2', a series combination of an external resistanceRb and supply voltage with polarity as indicated is connected. However, during motor mode this part of the circuit remains inactive. To initiate braking, the switch is thrown to position 2 and 2' at t = 0, thereby disconnecting the armature from the left hand supply. Here at t = 0+, the armature current will be Ia = (Eb + V)/(ra + Rb) as Eb and the right hand supply voltage have additive polarities by virtue
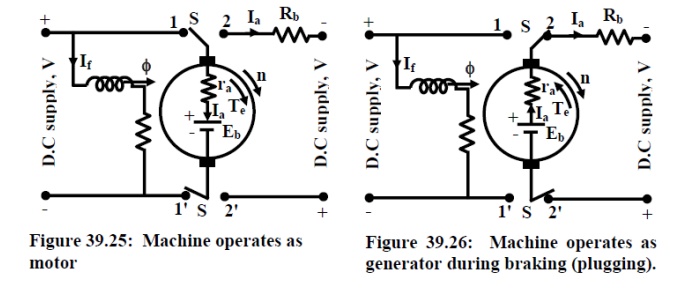
of the connection. Here also Ia reverses direction producing Te in opposite direction to n. Ia decreases as Eb decreases with time as speed decreases. However, Ia can not become zero at any time due to presence of supply V. So unlike rheostatic braking, substantial magnitude of braking torque prevails. Hence stopping of the motor is expected to be much faster then rheostatic breaking. But what happens, if S continuous to be in position 1' and 2' even after zero speed has been attained? The answer is rather simple, the machine will start picking up speed in the reverse direction operating as a motor. So care should be taken to disconnect the right hand supply, the moment armature speed becomes zero.
3. Regenerative braking
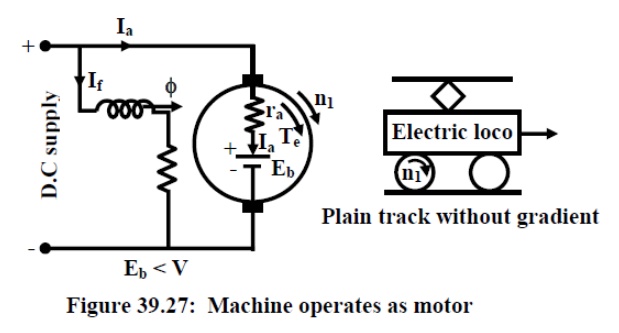
A machine operating as motor may go into regenerative braking mode if its speed becomes sufficiently high so as to make back emf greater than the supply voltage i.e., Eb > V. Obviously under this condition the direction of Ia will reverse imposing torque which is opposite to the direction of rotation. The situation is explained in figures 39.27 and 39.28. The normal motor operation is shown in figure 39.27 where armature motoring current Ia is drawn from the supply and as usual Eb < V. Since Eb = kŽå n1. The question is how speed on its own become large enough to make Eb < V causing regenerative braking. Such a situation may occur in practice when the mechanical load itself becomes active. Imagine the d.c motor is coupled to the wheel of locomotive which is moving along a plain track without any gradient as shown in figure 39.27. Machine is running as a motor at a speed of n1 rpm. However, when the track has a downward gradient, component of gravitational force along the track also
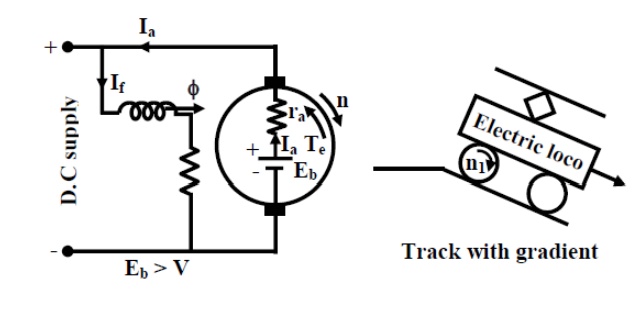
appears which will try to accelerate the motor and may increase its speed to n2 such that Eb = kŽå n2 > V. In such a scenario, direction of Ia reverses, feeding power back to supply. Regenerative braking here will not stop the motor but will help to arrest rise of dangerously high speed.
Related Topics