Repeated ranks, Example Solved Problems - SpearmanŌĆÖs Rank Correlation Coefficient | 12th Statistics : Chapter 4 : Correlation Analysis
Chapter: 12th Statistics : Chapter 4 : Correlation Analysis
SpearmanŌĆÖs Rank Correlation Coefficient
SPEARMANŌĆÖS RANK CORRELATION COEFFICIENT
If the data are in ordinal scale then SpearmanŌĆÖs rank correlation
coefficient is used. It is denoted by the Greek letter Žü (rho).
SpearmanŌĆÖs correlation can be calculated for the subjectivity data
also, like competition scores. The data can be ranked from low to high or high
to low by assigning ranks.
SpearmanŌĆÖs rank correlation coefficient is given by the formula
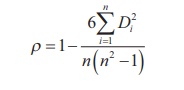
where Di = R1i ŌĆō R2i
R1i = rank of i in the first set of data
R2i = rank of i in the second set of data and
n = number of pairs of observations
Interpretation
SpearmanŌĆÖs rank correlation coefficient is a statistical measure
of the strength of a monotonic (increasing/decreasing) relationship between
paired data. Its interpretation is similar to that of PearsonŌĆÖs. That is, the
closer to the ┬▒1 means the stronger the monotonic relationship.
Example 4.3
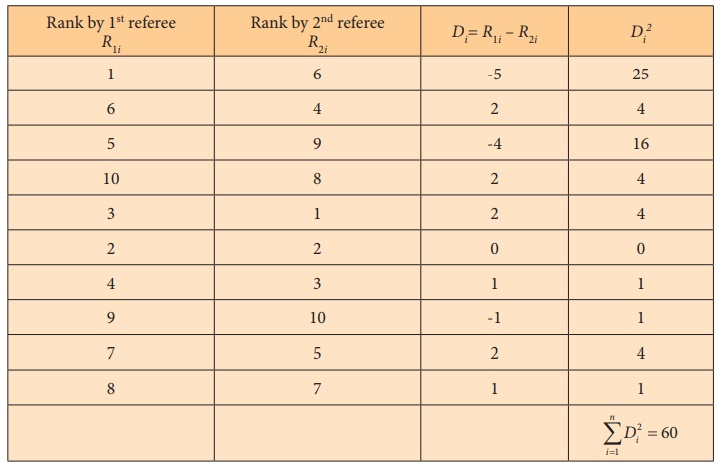
Two referees in a flower beauty competition rank the 10 types of
flowers as follows:

Use the rank correlation coefficient and find out what degree of
agreement is between the referees.
Solution:
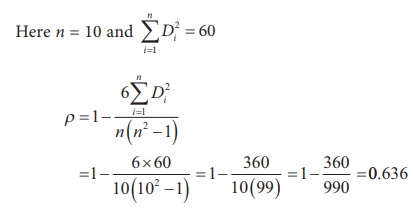
Interpretation: Degree of agreement between the referees ŌĆśAŌĆÖ and ŌĆśBŌĆÖ is 0.636 and they have ŌĆ£strong agreementŌĆØ in evaluating the competitors.
Example 4.4
Calculate the SpearmanŌĆÖs rank correlation coefficient for the
following data.

Solution:
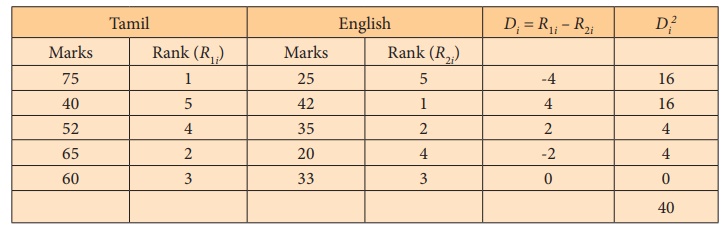
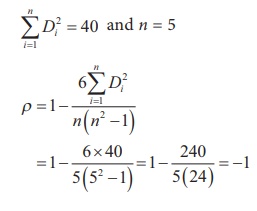
Interpretation: This perfect negative rank correlation (- 1)
indicates that scorings in the subjects, totally disagree. Student who
is best in Tamil is weakest in English subject and vice-versa.
Example 4.5
Quotations of index numbers of equity share prices of a certain
joint stock company and the prices of preference shares are given below.

Using the method of rank correlation determine the relationship
between equity shares and preference shares prices.
Solution:
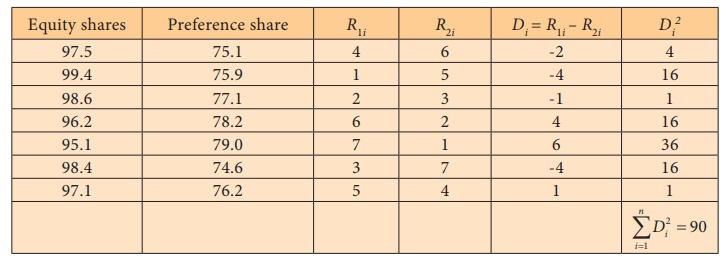

Interpretation: There is a negative correlation between equity
shares and preference share prices.
There is a strong disagreement between equity shares and
preference share prices.
Repeated ranks
When two or more items have equal values (i.e., a tie) it is
difficult to give ranks to them. In such cases the items are given the average
of the ranks they would have received. For example, if two
individuals are placed in the 8th place, they are given the rank [8+9] / 2 = 8.5 each, which is
common rank to be assigned and the next will be 10; and if three ranked equal
at the 8th place,
they are given the rank [8 + 9 +10] /3 = 9 which is the common rank to be assigned to
each; and the next rank will be 11.
In this case, a different formula is used when there is more than one item having the same value.

where mi is the number of repetitions of ith
rank
Example 4.6
Compute the rank correlation coefficient for the following data of
the marks obtained by 8 students in the Commerce and Mathematics.

Solution:
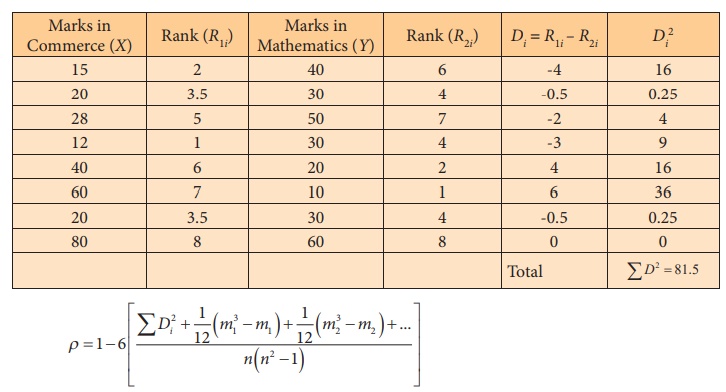
Repetitions of ranks
In Commerce (X), 20 is repeated two times corresponding to
ranks 3 and 4. Therefore, 3.5 is assigned for rank 2 and 3 with m1=2.
In Mathematics (Y), 30 is repeated three times
corresponding to ranks 3, 4 and 5. Therefore, 4 is assigned for ranks 3,4 and 5
with m2=3.
Therefore,
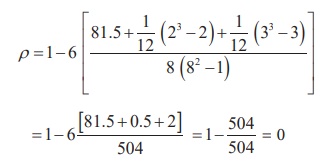
Interpretation: Marks in Commerce and Mathematics are
uncorrelated
Related Topics