Spearman’s Rank Correlation Coefficient

Rank correlation

Spearman’s Rank Correlation Coefficient

In 1904, Charles Edward Spearman, a British psychologist found out the method of ascertaining the coefficient of correlation by ranks. This method is based on rank. This measure is useful in dealing with qualitative characteristics, such as intelligence, beauty, morality, character, etc. It cannot be measured quantitatively, as in the case of Pearson’s coefficient of correlation.

Rank correlation is applicable only to individual observations. The result we get from this method is only an approximate one, because under ranking method original value are not taken into account. The formula for Spearman’s rank correlation which is denoted by ρ (pronounced as row) is

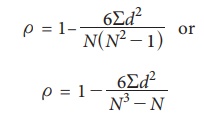
where          d = The difference of two ranks = R _X - R_Y and

N = Number of paired observations.

Rank coefficient of correlation value lies between –1 and +1. Symbolically, –1≤ρ≤+1

When we come across spearman’s rank correlation, we may find two types of problem

(i) When ranks are given

(ii) When ranks are not given

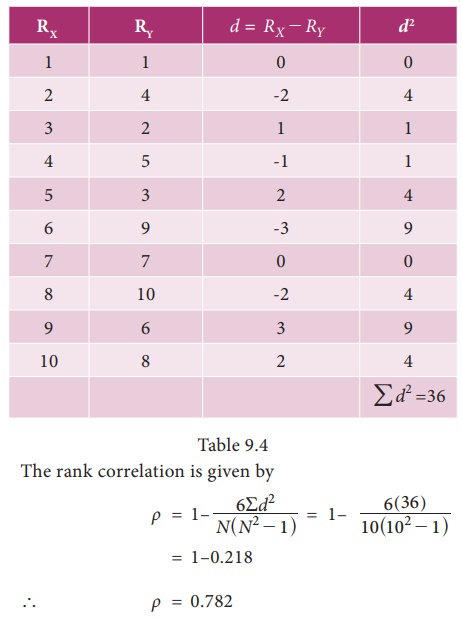
Example 9.6

The following are the ranks obtained by 10 students in Statistics and Mathematics

Find the rank correlation coefficient.

Solution:

Let R_X is considered for the ranks of Statistics and R_Y is considered for the ranks of mathematics.

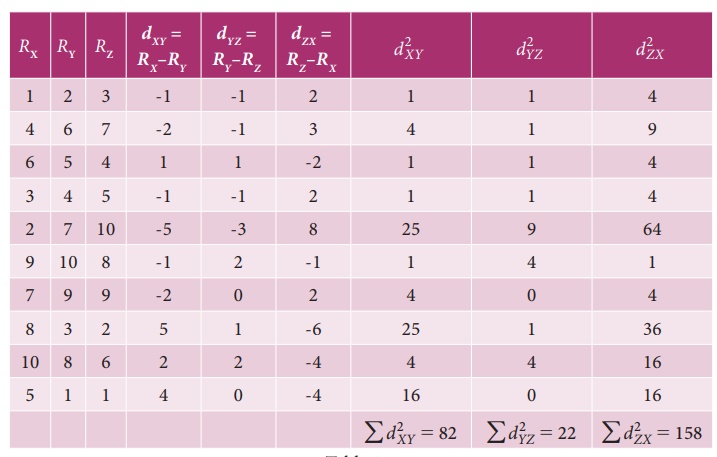
Example 9.7

Ten competitors in a beauty contest are ranked by three judges in the following order

Use the method of rank correlation coefficient to determine which pair of judges has the nearest approach to common taste in beauty?

Solution:

Let R_X,R_Y,R_Z denote the ranks by First judge, Second judge and third judge respectively

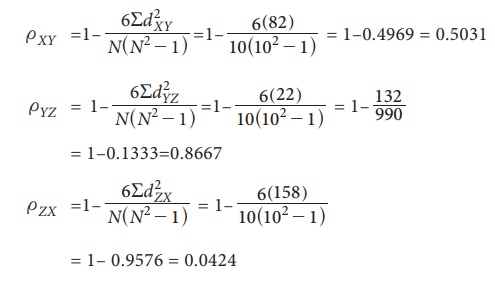
Since the rank correlation coefficient between Second and Third judges i.e., ρ_YZ is positive and weight among the three coefficients. So, Second judge and Third judge have the nearest approach for common taste in beauty.

Example 9.8

Calculate rank correlation coefficient of the following data

Solution:

Let X is considered for Subject1 and Y is considered for Subject2

Exercise 9.1

1. Calculate the correlation co-efficient for the following data

2. Find coefficient of correlation for the following:

3. Calculate coefficient of correlation for the ages of husbands and their respective wives:

4. Calculate the coefficient of correlation between X and Y series from the following data

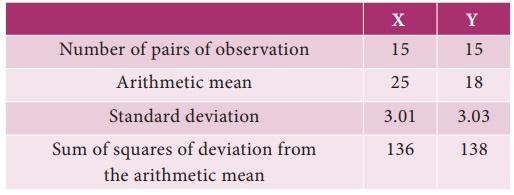
Summation of product deviations of X and Y series from their respective arithmetic means is 122.

5. Calculate correlation coefficient for the following data

6. Find coefficient of correlation for the following:

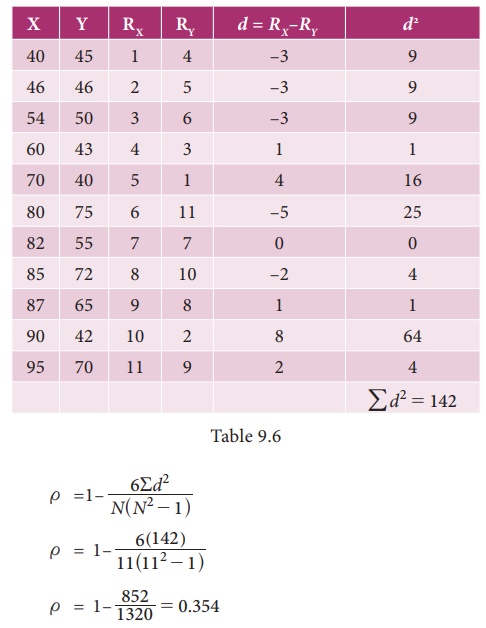
7. An examination of 11 applicants for a accountant post was taken by a finance company. The marks obtained by the applicants in the reasoning and aptitude tests are given below.

Calculate Spearman’s rank correlation coefficient from the data given above.

8. The following are the ranks obtained by 10 students in commerce and accountancy are given below

To what extent is the knowledge of students in the two subjects related?

9. A random sample of recent repair jobs was selected and estimated cost and actual cost were recorded.

Calculate the value of spearman’s correlation coefficient.

10. The rank of 10 students of same batch in two subjects A and B are given below. Calculate the rank correlation coefficient.