Maths - Correlation | 11th Business Mathematics and Statistics(EMS) : Chapter 9 : Correlation and Regression analysis
Chapter: 11th Business Mathematics and Statistics(EMS) : Chapter 9 : Correlation and Regression analysis
Correlation
Correlation
Introduction
In the
previous Chapter we have studied the characteristics of only one variable;
example, marks, weights, heights, rainfalls, prices, ages, sales, etc. This
type of analysis is called univariate analysis. Sometimes we may be interested
to find if there is any relationship between the two variables under study. For
example, the price of the commodity and its sale, height of a father and height
of his son, price and demand, yield and rainfall, height and weight and so on.
Thus the association of any two variables is known as correlation.

Correlation
is the statistical analysis which measures and analyses the degree or extent to
which two variables fluctuate with reference to each other.
1. Meaning of Correlation
The term
correlation refers to the degree of relationship between two or more variables.
If a change in one variable effects a change in the other variable, the
variables are said to be correlated.
2. Types of correlation
Correlation
is classified into many types, but the important are:
(i) Positive
(ii) Negative
Positive
and negative correlation depends upon the direction of change of the variables.
Positive Correlation
If two
variables tend to move together in the same direction that is, an increase in
the value of one variable is accompanied by an increase in the value of the
other variable; or a decrease in the value of one variable is accompanied by a
decrease in the value of the other variable, then the correlation is called
positive or direct correlation.
Example
(i) The
heights and weights of individuals
(ii) Price
and Supply
(iii) Rainfall
and Yield of crops
(iv) The
income and expenditure
Negative Correlation
If two variables tend to move
together in opposite direction so that an increase or decrease in the values of
one variable is accompanied by a decrease or increase in the value of the other
variable, then the correlation is called negative or inverse correlation.
Example
(i) Price
and demand
(ii) Repayment
period and EMI
(iii) Yield
of crops and price
No Correlation
Two
variables are said to be uncorrelated if the change in the value of one
variable has no connection with the change in the value of the other variable.
For example
We should
expect zero correlation (no correlation) between weight of a person and the
colour of his hair or the height of a person and the colour of his hair.
Simple correlation
The
correlation between two variables is called simple correlation. The correlation
in the case of more than two variables is called multiple correlation.
The following are the
mathematical methods of correlation coefficient
(i) Scatter
diagram
(ii) Karl
PearsonŌĆÖs Coefficient of Correlation
3. Scatter Diagram
Let (X1 , Y1),(X2,
Y2) ŌĆ” (X N
, YN) be the N pairs of observation of the variables X and Y. If we plot the values of X
along x - axis and the corresponding
values of Y along y-axis, the diagram so obtained is
called a scatter diagram. It gives us an idea of relationship between X and
Y. The type of scatter diagram under a simple linear correlation is given
below.

(i) If
the plotted points show an upward trend, the correlation will be positive.
(ii) If
the plotted points show a downward trend, the correlation will be negative.
(iii) If
the plotted points show no trend the variables are said to be uncorrelated.
4. Karl PearsonŌĆÖs Correlation Coefficient
Karl
Pearson, a great biometrician and statistician, suggested a mathematical method
for measuring the magnitude of linear relationship between two variables say X and Y. Karl PearsonŌĆÖs method is the most widely used method in practice
and is known as Pearsonian Coefficient of Correlation. It is denoted by the
symbol ŌĆśrŌĆÖ and defined as
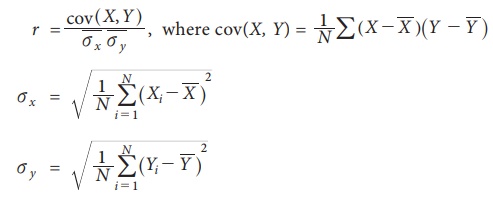
Hence the
formula to compute Karl Pearson Correlation coefficient is
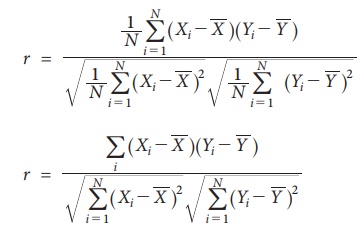
Interpretation of Correlation
coefficient:
Coefficient of correlation lies
between ŌĆō1 and +1. Symbolically, ŌĆō1Ōēż r
Ōēż + 1
┬Ę
When r
=+1 , then there is perfect positive correlation between the variables.
┬Ę
When r=ŌĆō1
, then there is perfect negative correlation between the variables.
┬Ę
When r=0,
then there is no relationship between the variables, that is the variables are
uncorrelated.
Thus, the
coefficient of correlation describes the magnitude and direction of
correlation.
Methods of computing Correlation Coefficient
(i) When deviations are taken from
Mean
Of all
the several mathematical methods of measuring correlation, the Karl PearsonŌĆÖs
method, popularly known as Pearsonian coefficient of correlation, is most
widely used in practice.

This
method is to be applied only when the deviations of items are taken from actual
means.
Steps to solve the problems:
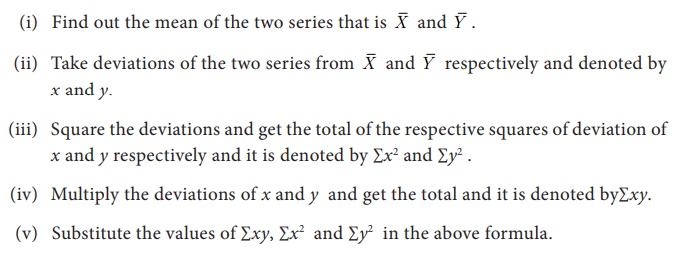
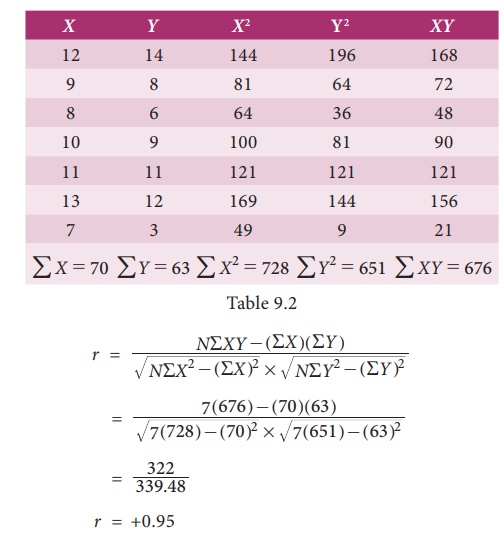
Example 9.1
Calculate
Karl PearsonŌĆÖs coefficient of correlation from the following data:

Solution:

(ii) When actual values are taken (without deviation)
when the
values of X and Y are considerably small in magnitude the following formula can be
used
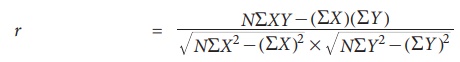
Example 9.2
Calculate
coefficient of correlation from the following data

Solution:
In both
the series items are in small number. Therefore correlation coefficient can
also be calculated without taking deviations from actual means or assumed mean.
(iii) When deviations are taken from an Assumed mean
When
actual means are in fractions, say the actual means of X and Y series are 20.167
and 29.23, the calculation of correlation by the method discussed above would
involve too many calculations and would take a lot of time. In such cases we
make use of the assumed mean method for finding out correlation. When
deviations are taken from an assumed mean the following formula is applicable:

Where dx = XŌĆōA and dy=YŌĆōB . Here A and B are assumed mean
NOTE
While applying assumed mean method, any value can be taken as
the assumed mean and the answer will be the same. However, the nearer the
assumed mean to the actual mean, the lesser will be the calculations.
Steps to solve the problems:
(i) Take
the deviations of X series from an
assumed mean, denote these deviations by dx
and obtain the total that is Rdx .
(ii) Take
the deviations of Y series from an
assumed mean, denote these deviations by dy
and obtain the total that is Rdy .
(iii) Square dx
and obtain the total Rdx2
.
(iv) Square
dy and obtain the total Rdy2 .
(v) Multiply
dx and dy and obtain the total Rdx dy
(vi) Substitute the values of R dxdy , R dx, R dy, R dx2 and R dy2 in the formula given above.
Example 9.3
Find out
the coefficient of correlation in the following case and interpret.

Solution:
Let us
consider Height of father (in inches) is represented as X and Height of son (in inches) is represented as Y
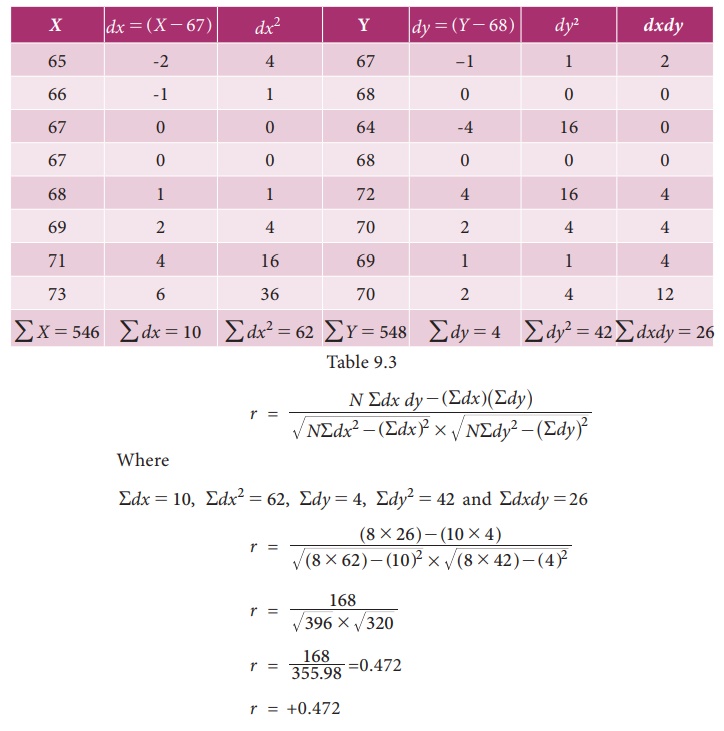
Heights
of fathers and their respective sons are positively correlated.
Example 9.4
Calculate
the correlation coefficient from the following data
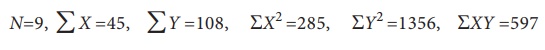
Solution
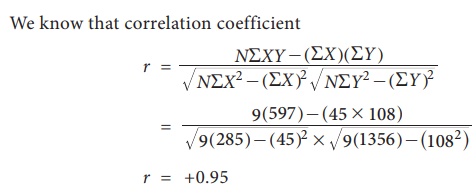
Example 9.5
From the
following data calculate the correlation coefficient Rxy =120, Rx2
=90, Ry2 =640
Solution:
Given Rxy =120, Rx2 =90, Ry2
=640
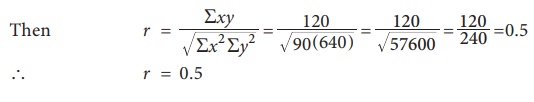
Related Topics