Regression Analysis

Regression Analysis

Introduction:

So far we have studied correlation analysis which measures the direction and strength of the relationship between two variables. Here we can estimate or predict the value of one variable from the given value of the other variable. For instance, price and supply are correlated. We can find out the expected amount of supply for a given price or the required price level for attaining the given amount of supply.

The term “ regression” literally means “ Stepping back towards the average”. It was first used by British biometrician Sir Francis Galton (1822 -1911), in connection with the inheritance of stature. Galton found that the offsprings of abnormally tall or short parents tend to “regress” or “step back” to the average population height. But the term “regression” as now used in Statistics is only a convenient term without having any reference to biometry.

Definition 9.1

Regression analysis is a mathematical measure of the average relationship between two or more variables in terms of the original units of the data.

1. Dependent and independent variables

Definition 9.2

In regression analysis there are two types of variables. The variable whose value is to be predicted is called dependent variable and the variable which is used for prediction is called independent variable.

Regression helps us to estimate the value of one variable, provided the value of the other variable is given. The statistical method which helps us to estimate the unknown value of one variable from the known value of the related variable is called Regression.

2. Regression Equations

Regression equations are algebraic expressions of the regression lines. Since there are two regression lines, there are two regression equations. The regression equation of X on Y is used to describe the variation in the values of X for given changes in Y and the regression equation of Y on X is used to describe the variation in the values of Y for given changes in X. Regression equations of (i) X on Y (ii) Y on X and their coefficients in different cases are described as follows.

Case 1:  When the actual values are taken

When we deal with actual values of X and Y variables the two regression equations and their respective coefficients are written as follows

(ii)  Regression Equation of X on Y;

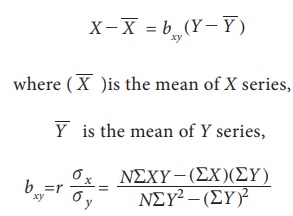
 is known as the regression coefficient of X on Y, and r is the correlation coefficient between X and Y, σ_x and σ_y are standard deviations of X and Y respectively.

(ii)  Regression Equation of Y on X;

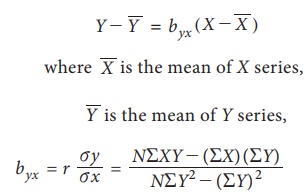
is known as the regression coefficient of X on  Y, and r is the correlation coefficient between X and Y, σ_x and σ_y are standard deviations of X and Y respectively.

Case 2  Deviations taken from Arithmetic means of X and Y

The calculation can very much be simplified instead of dealing with the actual values of X and Y, we take the deviations of X and Y series from their respective means. In such a case the two regression equations and their respective coefficients are written as follows:

(i) Regression Equation of X on Y:

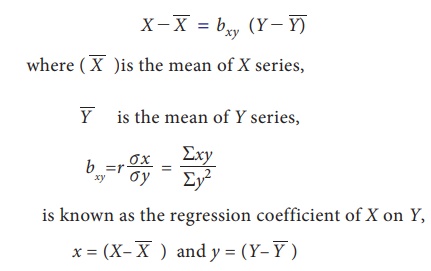
(ii)  Regression Equation of Y on X;

Note: Instead of finding out the values of correlation coefficient σ_x, σ_y, etc, we can find the value of regression coefficient by calculating ∑xy and ∑y2

Case 3  Deviations taken from Assumed Mean

When actual means of X and Y variables are in fractions the calculations can be simplified by taking the deviations from the assumed means. The regression equations and their coefficients are written as follows

(i) Regression Equation of Y on X

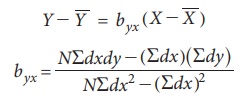
(ii) Regression Equation of X on Y

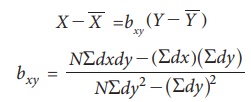
where dx=X–A, dy=Y–B, A and B are assumed means or arbitrary values are taken from X and Y respectively.

Properties of Regression Coefficients

(i) Correlation Coefficient is the geometric mean between the regression coefficients r = 

(ii) If one of the regression coefficients is greater than unity, the other must be less than unity.

(iii) Both the regression coefficients are of same sign.