Spearman’s Rank Correlation Coefficient

SPEARMAN’S RANK CORRELATION COEFFICIENT

If the data are in ordinal scale then Spearman’s rank correlation coefficient is used. It is denoted by the Greek letter ρ (rho).

Spearman’s correlation can be calculated for the subjectivity data also, like competition scores. The data can be ranked from low to high or high to low by assigning ranks.

Spearman’s rank correlation coefficient is given by the formula

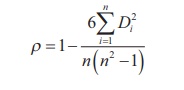
where D_i = R_1i – R_2i

R_1i = rank of i in the first set of data

R_2i = rank of i in the second set of data and

n = number of pairs of observations

Interpretation

Spearman’s rank correlation coefficient is a statistical measure of the strength of a monotonic (increasing/decreasing) relationship between paired data. Its interpretation is similar to that of Pearson’s. That is, the closer to the ±1 means the stronger the monotonic relationship.

Example 4.3

Two referees in a flower beauty competition rank the 10 types of flowers as follows:

Use the rank correlation coefficient and find out what degree of agreement is between the referees.

Solution:

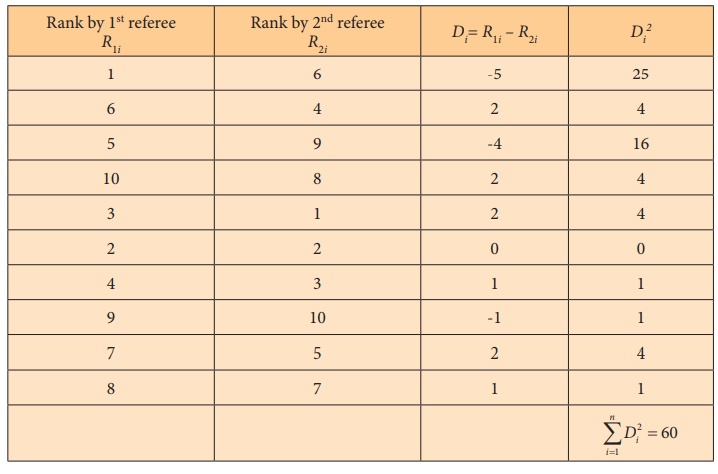
Interpretation: Degree of agreement between the referees ‘A’ and ‘B’ is 0.636 and they have  “strong agreement” in evaluating the competitors.

Example 4.4

Calculate the Spearman’s rank correlation coefficient for the following data.

Solution:

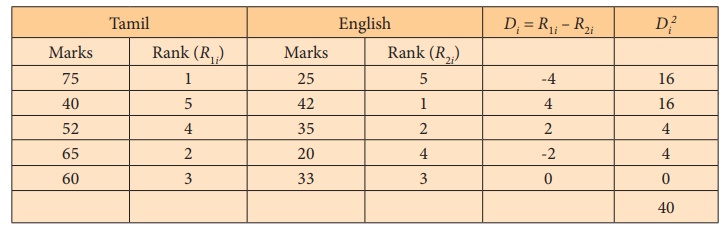
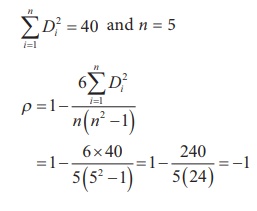
Interpretation: This perfect negative rank correlation (- 1) indicates that scorings in the subjects, totally disagree. Student who is best in Tamil is weakest in English subject and vice-versa.

Example 4.5

Quotations of index numbers of equity share prices of a certain joint stock company and the prices of preference shares are given below.

Using the method of rank correlation determine the relationship between equity shares and preference shares prices.

Solution:

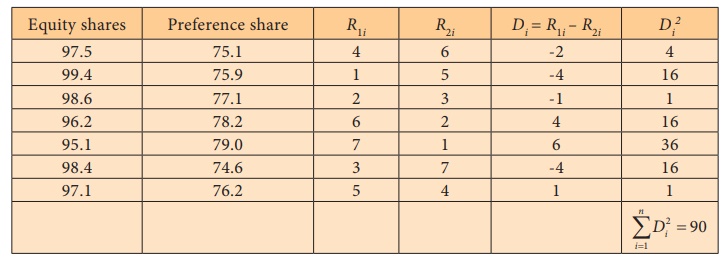
Interpretation: There is a negative correlation between equity shares and preference share prices.

There is a strong disagreement between equity shares and preference share prices.

Repeated ranks

When two or more items have equal values (i.e., a tie) it is difficult to give ranks to them. In such cases the items are given the average of the ranks they would have received. For example, if two individuals are placed in the 8^th place, they are given the rank [8+9] / 2 = 8.5 each, which is common rank to be assigned and the next will be 10; and if three ranked equal at the 8th place, they are given the rank [8 + 9 +10] /3  = 9 which is the common rank to be assigned to each; and the next rank will be 11. 

In this case, a different formula is used when there is more than one item having the same value. 

where m_i is the number of repetitions of i^th rank

Example 4.6

Compute the rank correlation coefficient for the following data of the marks obtained by 8 students in the Commerce and Mathematics.

Solution:

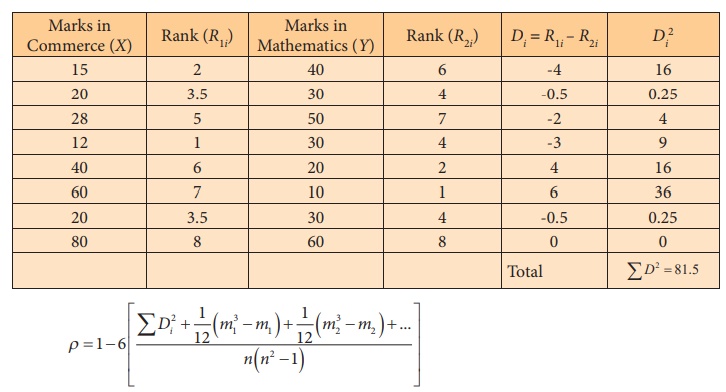
Repetitions of ranks

In Commerce (X), 20 is repeated two times corresponding to ranks 3 and 4. Therefore, 3.5 is assigned for rank 2 and 3 with m₁=2.

In Mathematics (Y), 30 is repeated three times corresponding to ranks 3, 4 and 5. Therefore, 4 is assigned for ranks 3,4 and 5 with m₂=3.

Therefore,

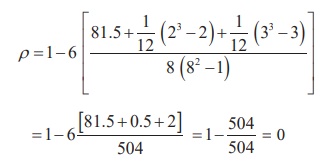
Interpretation: Marks in Commerce and Mathematics are uncorrelated