Solved Problems - Heat and Mass Transfer - Radiation

1. A black body at 3000 K emits radiation. Calculate the following:

i)       Monochromatic emissive power at 7 mm wave length.

ii)      Wave length at which emission is maximum.

iii)     Maximum emissive power.

iv)     Total emissive power,

v)      Calculate the total emissive of the furnace if it is assumed as a real surface having  emissivity equal to 0.85. Given: Surface temperature T = 3000K

2.The energy received by a 2 Â´2 m solar collector whose normal is inclined at 45°to the sun. The energy loss through the atmosphere is 50% and the diffuse radiation is 20% of direct radiation.

Given: Surface temperature T = 6000 K

Distance between earth and sun R = 12 Â´1010 m

Diameter on the sun D1 = 1.5 Â´109 m

Diameter of the earth D2 = 13.2 Â´106 m

3. A furnace wall emits radiation at 2000 K.Treating it as black body radiation, calculate

1.     Monochromatic radiant flux density at 1mm wave length.

2.     Wave length at which emission is maximum and the corresponding emissive power.

Total emissive power

Given: Temperature T = 2000 K; l= 1 mm = 1 Â´10-6

Solution:

1. Monochromatic emissive power (Ebl):

4. Calculate the heat exchange by radiation between the surfaces of two long cylindershaving radii 120mm and 60mm respectively. The axis of the cylinder is parallel to each other. The inner cylinder is maintained at a temperature of 130°C and emissivity of 0.6. Outer cylinder is maintained at a temperature of 30°C and emissivity of 0.5. (AU 2012)

Given: r1 = 60 mm = 0.060 m

r2= 120 mm

= 0.12

T1 = 130°C + 273

= 403

e1 = 0.6

T2= 30°C + 273 = 303 K

e2  = 0.5

To find: Heat exchange (Q)

Solution: Heat exchange between two large concentric cylinders is given by

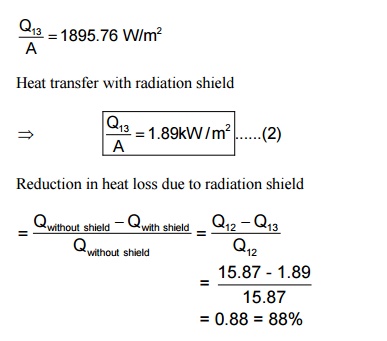
5. Emissivity's of two large parallel plates maintained at 800°C and 300°C are 0.5 respectively. Find net radiant hat exchange per square meter for these plates. Find the percentage reduction in heat transfer when a polished aluminums radiation shield of emissivity 0.06 is placed between them. Also find the temperature of the shield. (AU 2010)

Given: T1     = 800°C + 273

= 1073 K

T2= 300°C + 273

= 573 K

e1= 0.3  e2  = 0.5

Shield emissivity e3 = 0.06

To find:

1.  Net radiant heat exchange per square meter. (Q/A)

2.     Percentage reduction in heat loss due to radiation shield.

3.     Temperature of the shield (T3).

Solution: Heat exchange between two large parallel plates without radiation shield is given by

6. Two circular discs of diameter 20 cm each are placed 2 m apart. Calculate the radiant heat exchangefor these discs if there are maintained at 800°C and 300°C respectively and  the corresponding emissivity are 0.3 and 0.5.

Given:         D1 = 20 cm = 0.2 mD2 = 0.2 m       

          T1     = 800°C + 273    

                   = 1073 K   

          T2     = 300°C + 273    

                   = 573 K     

e1= 0.3e2 = 0.5

To find: Heat exchange (Q)

7. A long cylindrical heater 30 in diameter is maintained at 700°C. It has surface emissivity of 0.8. The heater is located in a large room whose wall is 35°C. Find the radiant heat transfer. Find the percentage of reduction in heat transfer if the heater is completely covered by radiation shield (e= 0.05) and diameter 40 mm.

Given: Diameter of cylinder D1=30mm=0.030 mm

Temperature         T1=700°C + 273 = 973 K      

Emissivity  e1 = 0.8               

Room temperature  T2 = 35°C + 273 = 308 K

Radiation Shield:

Emissivity e3 = 0.05

Diameter D3 = 40 mm = 0.040 m