Solar Radiation

Solar Radiation

The magnitude of the energy leaving the Sun varies with time and is closely associated with such factors as solar flares and sunspots. Nevertheless, we often choose to work with an average value. The energy leaving the sun is emitted outward in all directions so that at any particular distance from the Sun we may imagine the energy being dispersed over an imaginary spherical area. Because this area increases with the distance squared, the solar flux also decreases with the distance squared. At the average distance between Earth and Sun this heat flux is 1353 W/m2, so that the average heat flux on any object in Earth orbit is found as:

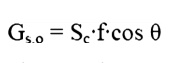
Where Sc = Solar Constant, 1353 W/m2

f = correction factor for eccentricity in Earth Orbit, (0.97<f<1.03)

θ            =   Angle   of   surface   from   normal   to   Sun.

Because of reflection and absorption in the reduced at ground level. Nevertheless, this value gives us some opportunity to estimate the

potential for using solar energy, such as in photovoltaic cells.

Some Definitions

In the previous section we introduced the Stefan-Boltzman Equation to describe radiation from an ideal surface.

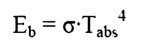
This equation provides a method of determining the total energy leaving a surface, but gives no indication of the direction in which it travels. As we continue our study, we will want to be able to calculate how heat is distributed among various objects.

For this purpose, we will introduce the radiation intensity, I, defined as the energy emitted per unit area, per unit time, per unit solid angle. Before writing an equation for this new property, we will need to define some of the terms we will be using.

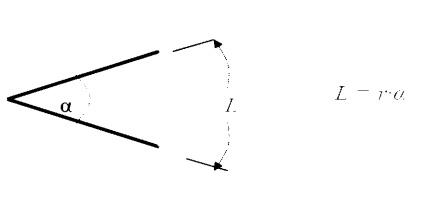
Angles and Arc Length

We are well accustomed to thinking of an angle as a two dimensional object. It may be used to find an arc length:

Solid Angle

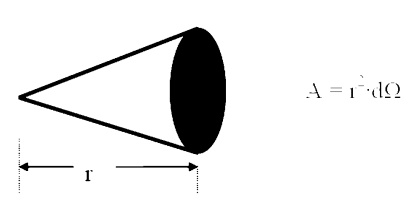
We generalize the idea of an angle and an arc length to three dimensions and define a solid

angle, Ω, which like the standard angle has n the radius squared will have dimensions of length squared, or area, and will have the magnitude of the encompassed area.

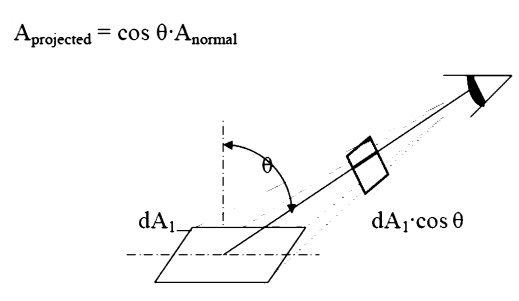
Projected Area

The area, dA1, as seen from the prospective o to the surface, will appear somewhattermed thesmaller projected area.

Intensity

The ideal intensity, Ib, may now be defined as the energy emitted from an ideal body, per unit projected area, per unit time, per unit solid angle.

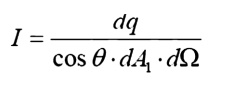
Spherical Geometry

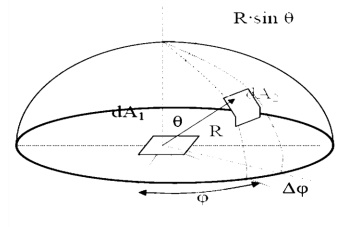
Since any surface will emit radiation outward in all directions above the surface, the spherical coordinate system provides a convenient tool for analysis. The three basic coordinates shown are

R,      φ,   and   θ,   representing   the   radial,   azimuth

In general dA1 will correspond to the emitting surface or the source. The surface dA2 will correspond to the receiving surface or the target. Note that the area proscribed on the hemisphere, dA2 , may be written as:

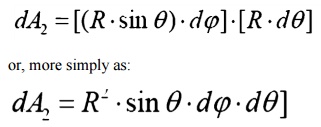
Recalling the definition of the solid angle,

dA = R2·dΩ

we find that:

dΩ     =sin2R   θ·dθ·dφ

Real Surfaces

Thus far we have spoken of ideal surfaces, i.e. those that emit energy according to the Stefan-Boltzman law:

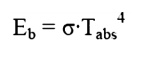
Real surfaces have emissive powers, E, which are somewhat less than that obtained theoretically

by     Boltzman.   To   account   for   this   reduction,   w

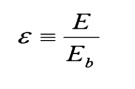
so that the emissive power from any real surface is given by:

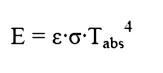
Receiving Properties

Targets receive radiation in one of three ways; they absorption, reflection or transmission. To account for these characteristics, we introduce three additional properties:

•             Absorptivity,   α,   the   fraction   of   incident   r

•             Reflectivity,   ρ,   the   fraction   of   incident   r

Transmissivity,onofincident radiationτ, thetransmittedfracti.

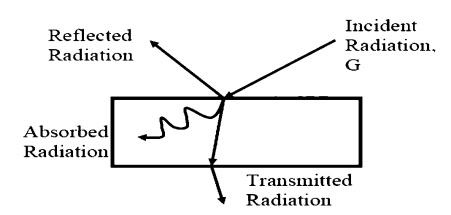
We see, from Conservation of Energy, that:

α    +   ρ   +   τ   =   1

In      this   course,   we   will   deal   with   only   opaque

α    +   ρ   =   1                                  Opaque Surfaces