Chapter: Mechanical : Heat and Mass Transfer : Radiation
Radiation
RADIATION :
BLACK BODY RADIATION:
Definition:
Radiation is the energy
transfer across a system boundary due to a T, by the mechanism of photon
emission or electromagnetic wave emission.
Because the mechanism
of transmission is photon emission, unlike conduction and convection, there
need be no intermediate matter to enable transmission.
The significance of
this is that radiation will be the only mechanism for heat transfer whenever a
vacuum is present.
Electromagnetic Phenomena.
We are well acquainted
with a wide range of electromagnetic phenomena in modern life. These phenomena
are sometimes thought of as wave phenomena and are, consequently, often
described
in
terms of electromagnetic wave length, ╬╗. E shown below:

One aspect of
electromagnetic radiation is that the related topics are more closely
associated with optics and electronics than with those normally found in
mechanical engineering courses. Nevertheless, these are widely encountered
topics and the student is familiar with them through every day life
experiences.
From a viewpoint of
previously studied topics students, particularly those with a background in
mechanical or chemical engineering, will find the subject of Radiation Heat
Transfer a little unusual. The physics background differs fundamentally from
that found in the areas of continuum mechanics. Much of the related material is
found in courses more closely identified with quantum physics or electrical
engineering, i.e. Fields and Waves. At this point, it is important for us to
recognize that since the subject arises from a different area of physics, it
will be important that we study these concepts with extra care.
Stefan-Boltzman Law
Both Stefan and Boltzman were physicists; any
student taking a course in quantum physics will
become well acquainted
with BoltzmanÔÇÖs work as he to the field. Both were contemporaries of Einstein
so we see that the subject is of fairly recent
vintage.
(Recall that the basic equation for convection heat transfer is attributed to
Newton)
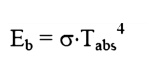
where: Eb = Emissive Power, the gross
energy emitted from an ideal surface per unit area, time.
Ôőů
-8 2Ôőů4
¤â
=
Stefan Boltzman10W/mK
constant, 5.67
Tabs = Absolute temperature of the
emitting surface, K.
Take particular note of
the fact that absolute temperatures are used in Radiation. It is suggested, as
a matter of good practice, to convert all temperatures to the absolute scale as
an initial step in all radiation problems.
You will notice that
the equation does not in the emissive power. The relationship between these
terms is as follows. Consider two infinite
plane
surfaces, both facing one another. Both surfaces are ideal surfaces. One
surface is found to be at temperature, T1, the other at temperature, T2. Since
both temperatures are at temperatures above absolute zero, both will radiate
energy as described by the Stefan-Boltzman law. The heat flux will be the net
radiant flow as given by:

PlankÔÇÖs Law
While the Stefan-Boltzman law is useful for studying
overall energy emissions, it does not allow
us
to treat those interactions, which deal specifically with wavelength, overcome
by another of the modern physicists, Max Plank, who developed a relationship
for wave-based emissions.

We havenÔÇÖt yet
defined the b╬╗.MonochromaticAnimplicitdefinitionis Emi
provided
by the following equation:
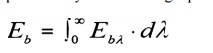
We
may view this equation graphically as follows:

A
definition of monochromatic Emissive Power would be obtained by differentiating
the integral equation:

The actual
form of PlankÔÇÖs
law is:
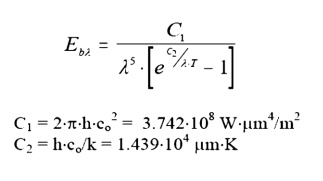
Where: h, co,
k are all parameters from quantum physics. We need not worry about their
precise definition here.
This equation may be solved at any T, ╬╗ to give the value of the monochromatic emissivity at that
that condition. Alternatively, the
function may be
substituted into the
integral
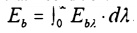
to
find the Emissive power for any temperature. While performing this integral by
hand is difficult, students may readily evaluate the integral through one of
several computer programs, i.e. MathCad, Maple, Mathmatica, etc.
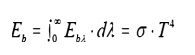
Emission Over Specific Wave Length Bands
Consider the problem of
designing a tanning machine. As a part of the machine, we will need to design a
very powerful incandescent light source. We may wish to know how much energy is
being emitted over the
ultraviolet
band (10-4 to 0.4 ╬╝m),
known to be
particularly dangerous.

With
a computer available, evaluation of this integral is rather trivial.
Alternatively, the text books provide a table of integrals. The format used is
as follows:
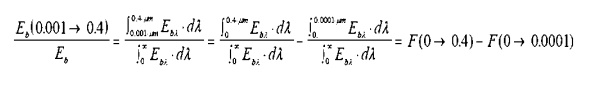
Referring to such
tables, we see the last two functions listed in the second column. In the first
column is aÔőůT.
Thisparameter,isfoundbytakingthe product╬╗ of the absolute temperature of
the
emitting surface, T, and the upper limit incandescent bulb is designed to
operate at a temperature of 2000K. Reading from the table:
╬╗.,

This
is the fraction of the total energy emitted which falls within the IR band. To
find the absolute energy emitted multiply this value times the total energy
emitted:
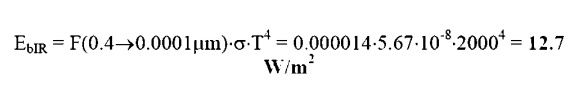
Solar Radiation
The
magnitude of the energy leaving the Sun varies with time and is closely
associated with such factors as solar flares and sunspots. Nevertheless, we
often choose to work with an average value. The energy leaving the sun is
emitted outward in all directions so that at any particular distance from the
Sun we may imagine the energy being dispersed over an imaginary spherical area.
Because this area increases with the distance squared, the solar flux also
decreases with the distance squared. At the average distance between Earth and
Sun this heat flux is 1353 W/m2, so that the average heat flux on any object in
Earth orbit is found as:
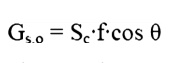
Where Sc = Solar Constant, 1353 W/m2
f = correction factor for eccentricity in Earth
Orbit, (0.97<f<1.03)
╬Ş
=
Angle of surface
from normal to
Sun.
Because of reflection
and absorption in the reduced at ground level. Nevertheless, this value gives
us some opportunity to estimate the
potential for using solar energy, such as in
photovoltaic cells.
Some Definitions
In
the previous section we introduced the Stefan-Boltzman Equation to describe
radiation from an ideal surface.
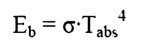
This equation provides
a method of determining the total energy leaving a surface, but gives no
indication of the direction in which it travels. As we continue our study, we
will want to be able to calculate how heat is distributed among various
objects.
For this purpose, we
will introduce the radiation intensity, I, defined as the energy emitted per
unit area, per unit time, per unit solid angle. Before writing an equation for
this new property, we will need to define some of the terms we will be using.
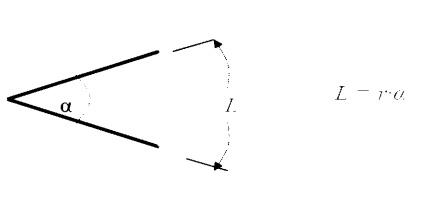
Angles
and Arc Length
We
are well accustomed to thinking of an angle as a two dimensional object. It may
be used to find an arc length:
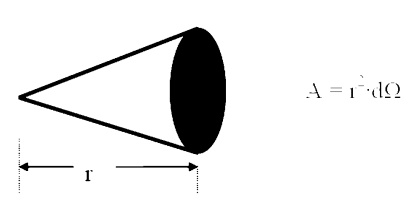
Solid Angle
We generalize the idea of an angle and an arc length
to three dimensions and define a solid
angle, ╬ę, which like
the standard angle has n the radius squared will have dimensions of length
squared, or area, and will have the magnitude of the encompassed area.
Projected Area
The area, dA1, as seen
from the prospective o to the surface, will appear somewhattermed thesmaller
projected area.
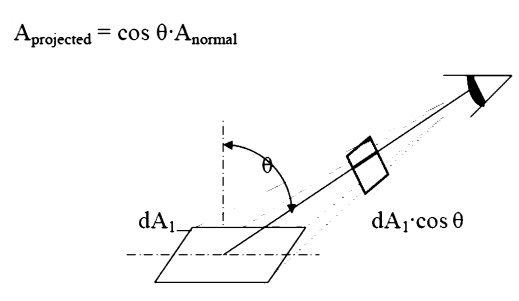
Intensity
The ideal intensity,
Ib, may now be defined as the energy emitted from an ideal body, per unit
projected area, per unit time, per unit solid angle.
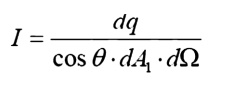
Spherical Geometry
Since any surface will
emit radiation outward in all directions above the surface, the spherical
coordinate system provides a convenient tool for analysis. The three basic
coordinates shown are
R, ¤ć, and
╬Ş, representing the
radial, azimuth
In general dA1 will
correspond to the emitting surface or the source. The surface dA2 will
correspond to the receiving surface or the target. Note that the area
proscribed on the hemisphere, dA2 , may be written as:
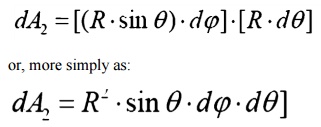
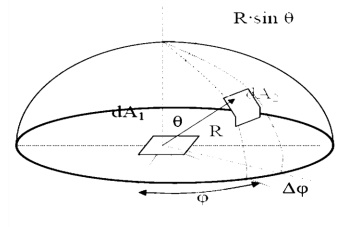
Recalling the definition of the solid angle,
dA = R2┬Ěd╬ę
we find that:
d╬ę =sin2R ╬Ş┬Ěd╬Ş┬Ěd¤ć
Real Surfaces
Thus far we have spoken of ideal
surfaces, i.e. those that emit energy according to the Stefan-Boltzman law:
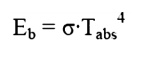
Real surfaces have emissive powers, E, which are
somewhat less than that obtained theoretically
by Boltzman. To
account for this
reduction, w
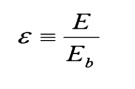
so that the emissive power from any real
surface is given by:
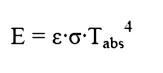
Receiving Properties
Targets receive
radiation in one of three ways; they absorption, reflection or transmission. To
account for these characteristics, we introduce three additional properties:
ÔÇó
Absorptivity, ╬▒,
the fraction of
incident r
ÔÇó
Reflectivity, ¤ü,
the fraction of
incident r
Transmissivity,onofincident radiation¤ä,
thetransmittedfracti.
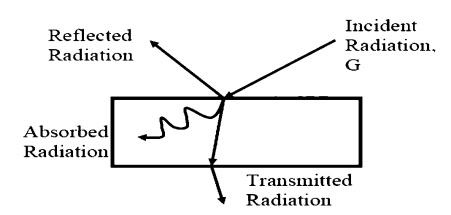
We see, from Conservation of Energy, that:
╬▒ + ¤ü
+ ¤ä = 1
In this course,
we will deal
with only opaque
╬▒ +
¤ü = 1 Opaque
Surfaces
SHAPE FACTOR:
Net Exchange Between Surfaces

Net Energy Leaving a Surface

ELECTRICAL ANALOGY :
Electrical Analogy for Radiation
We may develop an electrical analogy for
radiation, similar to that produced for conduction. The two analogies should
not be mixed: they have different dimensions on the potential differences, resistance
and current flows.

RADIATION SHIELDS ;
Insulated surfaces. In steady state heat
transfer, a surface cannot receive net energy if it is insulated. Because the
energy cannot be stored by a surface in steady state, all energy must be
re-radiated back into the enclosure. Insulated surfaces are often termed as
re-radiating surfaces.
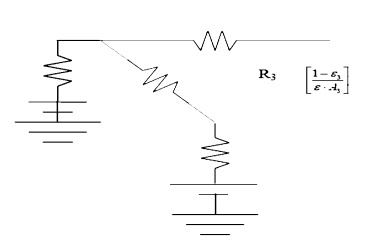
Electrically cannot flow through a battery if it is
not grounded.
Surface 3 is not
grounded so that the battery and surface resistance serve no purpose and are
removed from the drawing.
ÔÇó
Black
surfaces: A black,
or ideal surface,
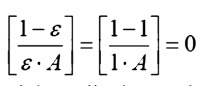
In this case the nodal Radiosity and emissive power
will be equal.
This result gives some
insight into the physical meaning of a black surface. Ideal surfaces radiate at
the maximum possible level. Non-black surfaces will have a reduced potential,
somewhat like a battery with a corroded terminal. They therefore have a reduced
potential to cause heat/current flow.
ÔÇó Largeces: Surfacessurfahaving
a large surface area will behave as black surfaces, irrespective of the actual
surface properties:
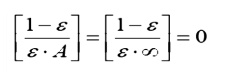
Physically, this corresponds to the
characteristic of large surfaces that as they reflect energy, there is very
little chance that energy will strike the smaller surfaces; most of the energy
is reflected back to another part of the same large surface. After several
partial absorptions most of the energy received is absorbed.
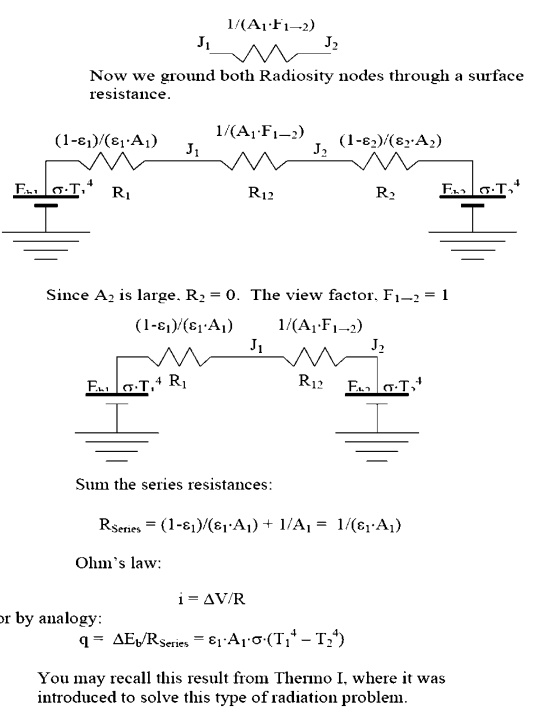
Consider the case of an object, 1,
placed inside a large enclosure, 2. The system will consist of two objects, so
we proceed to construct a circuit with two radiosity nodes
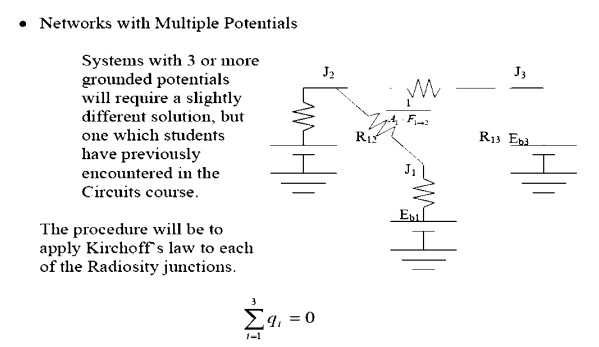
In this example there
are three junctions, so we will obtain three equations. This will allow us to
solve for three unknowns.
Radiation problems will generally be presented on
one of two ways:
1. The
surface net heat flow is given and the surface temperature is to be found.
2. The
surface temperature is given and the net heat flow is to be found.
Returning for a moment
to the coal grate furnace, let us assume that we know (a) the total heat being
produced by the coal bed, (b) the temperatures of the water walls and (c) the
temperature of the super heater sections.
Apply KirchoffÔÇÖs law
about node 1,
for the co
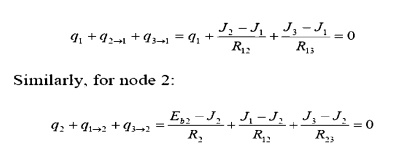
(Note how node 1, with
a specified heat input, is handled differently than node 2, with a specified
temperature.
And for node 3:
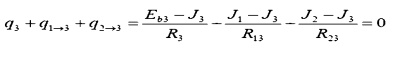
The three equations must be solved
simultaneously. Since they are each linear in J, matrix methods may be used:
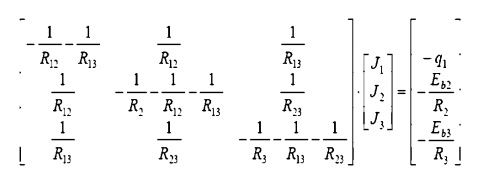
The matrix may be
solved for the individual Radiosity. Once these are known, we return to the
electrical analogy to find the temperature of surface 1, and the heat flows to
surfaces 2 and 3.
Surface 1: Find the coal bed
temperature, given the heat flow:
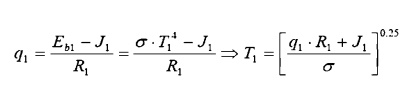
Surface 2: Find the water wall heat
input, given the water wall temperature:
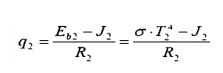
Surface 3: (Similar to surface 2) Find
the water wall heat input, given the water wall temperature:

Related Topics