Chapter: Mechanical : Heat and Mass Transfer : Radiation
Radiation Shields
RADIATION SHIELDS ;
Insulated surfaces. In steady state heat transfer, a surface cannot receive net energy if it is insulated. Because the energy cannot be stored by a surface in steady state, all energy must be re-radiated back into the enclosure. Insulated surfaces are often termed as re-radiating surfaces.
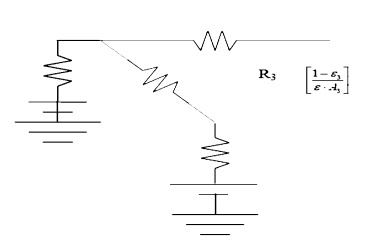
Electrically cannot flow through a battery if it is not grounded.
Surface 3 is not grounded so that the battery and surface resistance serve no purpose and are removed from the drawing.
ÔÇó Black surfaces: A black, or ideal surface,
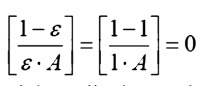
In this case the nodal Radiosity and emissive power will be equal.
This result gives some insight into the physical meaning of a black surface. Ideal surfaces radiate at the maximum possible level. Non-black surfaces will have a reduced potential, somewhat like a battery with a corroded terminal. They therefore have a reduced potential to cause heat/current flow.
ÔÇó Largeces: Surfacessurfahaving a large surface area will behave as black surfaces, irrespective of the actual surface properties:
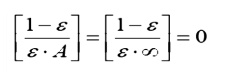
Physically, this corresponds to the characteristic of large surfaces that as they reflect energy, there is very little chance that energy will strike the smaller surfaces; most of the energy is reflected back to another part of the same large surface. After several partial absorptions most of the energy received is absorbed.
Consider the case of an object, 1, placed inside a large enclosure, 2. The system will consist of two objects, so we proceed to construct a circuit with two radiosity nodes
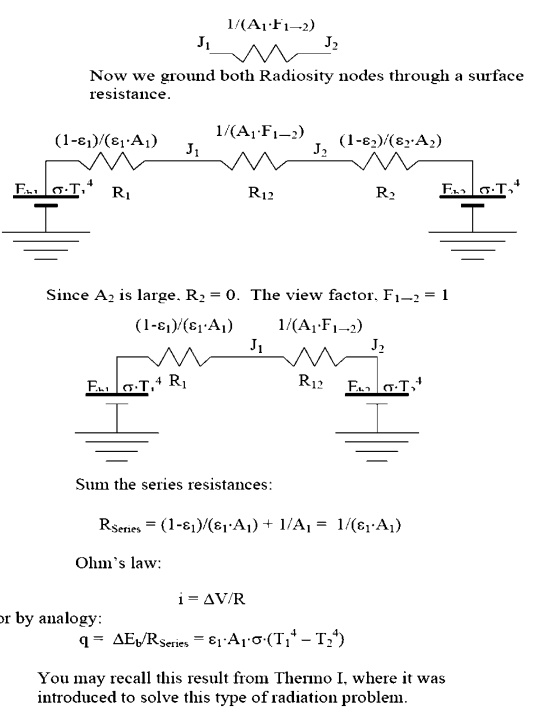
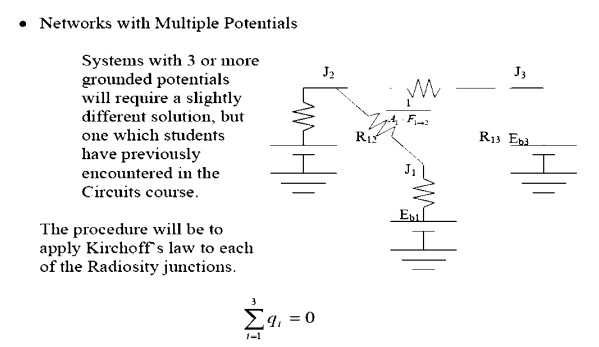
In this example there are three junctions, so we will obtain three equations. This will allow us to solve for three unknowns.
Radiation problems will generally be presented on one of two ways:
1. The surface net heat flow is given and the surface temperature is to be found.
2. The surface temperature is given and the net heat flow is to be found.
Returning for a moment to the coal grate furnace, let us assume that we know (a) the total heat being produced by the coal bed, (b) the temperatures of the water walls and (c) the temperature of the super heater sections.
Apply KirchoffÔÇÖs law about node 1, for the co
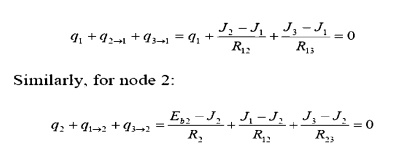
(Note how node 1, with a specified heat input, is handled differently than node 2, with a specified temperature.
And for node 3:
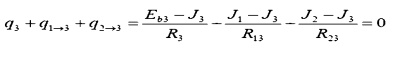
The three equations must be solved simultaneously. Since they are each linear in J, matrix methods may be used:
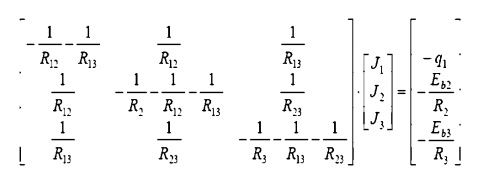
The matrix may be solved for the individual Radiosity. Once these are known, we return to the electrical analogy to find the temperature of surface 1, and the heat flows to surfaces 2 and 3.
Surface 1: Find the coal bed temperature, given the heat flow:
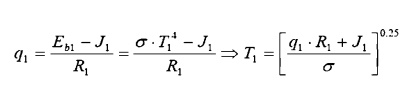
Surface 2: Find the water wall heat input, given the water wall temperature:
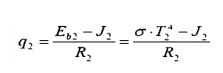
Surface 3: (Similar to surface 2) Find the water wall heat input, given the water wall temperature:

Related Topics