Shape Factor

SHAPE FACTOR:

Net Exchange Between Surfaces

Net Energy Leaving a Surface

ELECTRICAL ANALOGY :

Electrical Analogy for Radiation

We may develop an electrical analogy for radiation, similar to that produced for conduction. The two analogies should not be mixed: they have different dimensions on the potential differences, resistance and current flows.

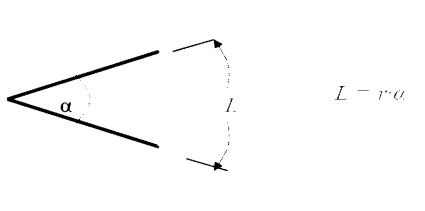
Angles and Arc Length

We are well accustomed to thinking of an angle as a two dimensional object. It may be used to find an arc length:

Solid Angle

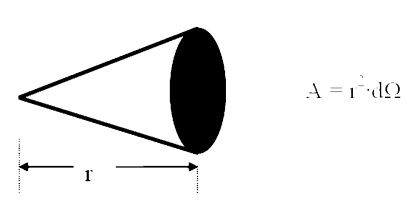
We generalize the idea of an angle and an arc length to three dimensions and define a solid

angle, Ω, which like the standard angle has n the radius squared will have dimensions of length squared, or area, and will have the magnitude of the encompassed area.

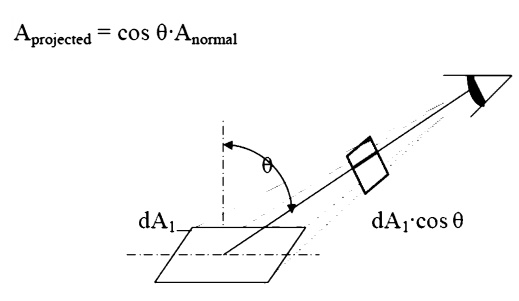
Projected Area

The area, dA1, as seen from the prospective o to the surface, will appear somewhattermed thesmaller projected area.

Intensity

The ideal intensity, Ib, may now be defined as the energy emitted from an ideal body, per unit projected area, per unit time, per unit solid angle.

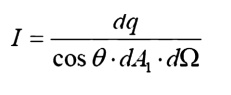
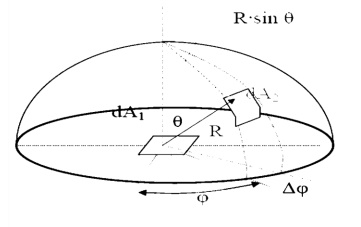
Spherical Geometry

Since any surface will emit radiation outward in all directions above the surface, the spherical coordinate system provides a convenient tool for analysis. The three basic coordinates shown are

R,      φ,   and   θ,   representing   the   radial,   azimuth

In general dA1 will correspond to the emitting surface or the source. The surface dA2 will correspond to the receiving surface or the target. Note that the area proscribed on the hemisphere, dA2 , may be written as:

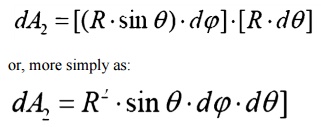
Recalling the definition of the solid angle,

dA = R2·dΩ

we find that:

dΩ     =sin2R   θ·dθ·dφ

Real Surfaces

Thus far we have spoken of ideal surfaces, i.e. those that emit energy according to the Stefan-Boltzman law:

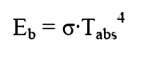
Real surfaces have emissive powers, E, which are somewhat less than that obtained theoretically

by     Boltzman.   To   account   for   this   reduction,   w

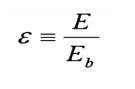
so that the emissive power from any real surface is given by:

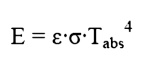
Receiving Properties

Targets receive radiation in one of three ways; they absorption, reflection or transmission. To account for these characteristics, we introduce three additional properties:

•             Absorptivity,   α,   the   fraction   of   incident   r

•             Reflectivity,   ρ,   the   fraction   of   incident   r

Transmissivity,onofincident radiationτ, thetransmittedfracti.

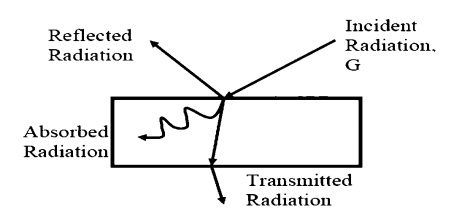
We see, from Conservation of Energy, that:

α    +   ρ   +   τ   =   1

In      this   course,   we   will   deal   with   only   opaque

α    +   ρ   =   1                                  Opaque Surfaces