Solved Problems - Electromechanical Energy Conversion and Concepts in Rotating Machines

SOLVED PROBLEMS

Example 1:

An actuator with a rotating vane is shown in Fig. 3.26. You may assume that the permeability of both the core and the vane are infinite ( μ -> ¥ ). The total air-gap length is 2g and shape of the vane is such that the effective area of the air gap can be assumed to be of the form

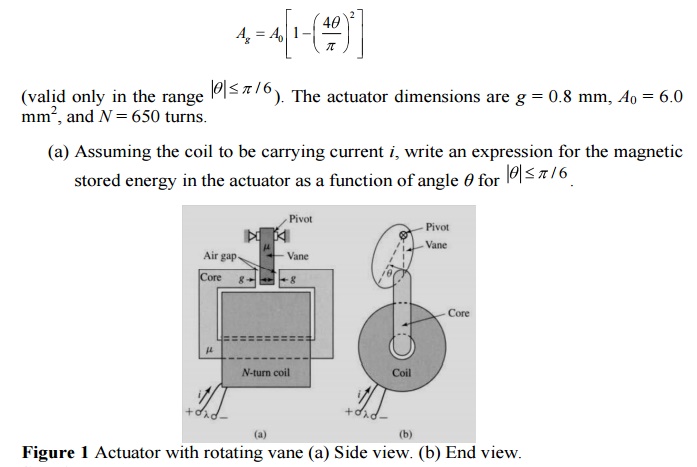
Example 2:

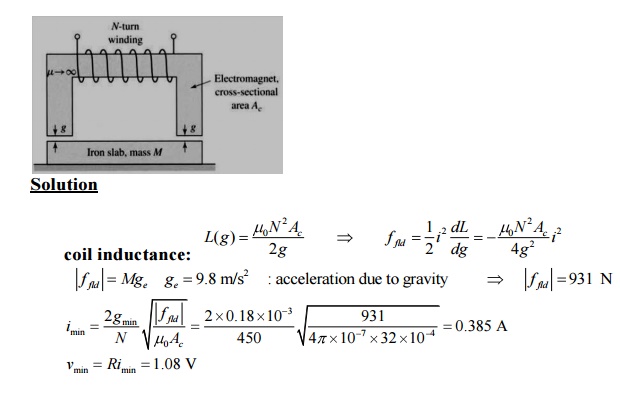
As shown in Fig. 2, an N-turn (N = 100) electromagnet is to be used to lift a slab of iron of mass M. The surface roughness of the iron is such that when the iron and the electromagnet are in contact, there is a minimum air gap of g_min = 0.18 mm in each leg. The electromagnet cross-sectional area A_c = 32 cm² and coil resistance is 2.8 Ω. Calculate the minimum coil voltage which must be used to lift a slab of mass 95 kg against the force of gravity. Neglect the reluctance of the iron.

Example :3

An inductor is made up of a 525-turn coil on a core of 14-cm² cross-sectional area and gap length 0.16 mm. The coil is connected directly to a 120-V 60-Hz voltage source. Neglect the coil resistance and leakage inductance. Assuming the coil reluctance to be negligible, calculate the time-averaged force acting on the core tending to close the air gap. How would this force vary if the air-gap length were doubled?

Solution

Example 5:

Two windings, one mounted on a stator and the other on a rotor, have self- and mutual inductances of

L₁₁= 4.5 H                          

L₂₂= 2.5 H                          

L₁₂ = 2.8cosθ  H

where θ is the angle between the axes of the windings. The resistances of the windings may be neglected. Winding 2 is short-circuited, and the current in winding 1 as a function of time is i_l = 10 sin ωt A.

a. Derive an expression for the numerical value in newton-meters of the instantaneous torque on the rotor in terms of the angle θ.

b.              Compute the time-averaged torque in newton-meters when θ = 45°.

If the rotor is allowed to move, will it rotate continuously or will it tend to come to rest? If the latter, at what value of θ₀ ?

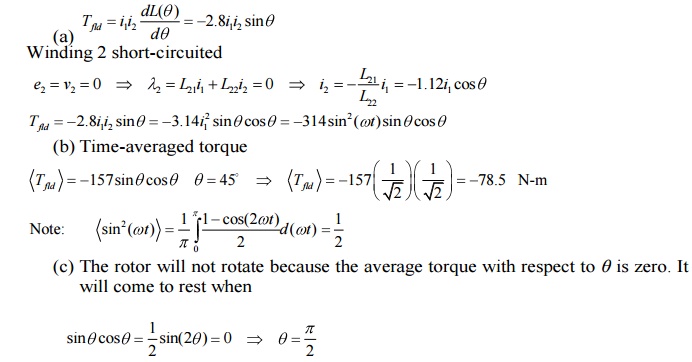
Example 6:

A loudspeaker is made of a magnetic core of infinite permeability and circular symmetry, as shown in Figs. 3.37a and b. The air-gap length g is much less than the radius r₀ of the central core. The voice coil is constrained to move only in the x direction and is attached to the speaker cone, which is not shown in the figure. A constant radial magnetic field is produced in the air gap by a direct current in coil 1, i_l = I₁. An audio-frequency signal i₂ = I₂ cos(ωt) is then applied to the voice coil. Assume the voice coil to be of negligible thickness and composed of N₂ turns uniformly distributed over its height h. Also assume that its displacement is such that it remains in the air gap (0 £ x £ l-h)

(a)                Calculate the force on the voice coil, using the Lorentz Force Law (Eq. 3.1).

(b)                Calculate the self-inductance of each coil.

(c)  Calculate the mutual inductance between the coils. (Hint: Assume that current is applied to the voice coil, and calculate the flux linkages of coil 1. Note that these flux linkages vary with the displacement x.

(d) Calculate the force on the voice coil from the coenergy Wfld .