Chapter: Electrical machines : Electromechanical Energy Conversion and Concepts in Rotating Machines
Force In A Singly Excited Magnetic Field System
Force In A Singly Excited Magnetic Field System
1. Model& Analysis
The conversion of electrical energy to mechanical energy follows the law of conservation of energy. In general, the law of conservation of energy states that energy is neither created nor destroyed. Equation (1) describes the process of electromechanical energy conversion for a differential time interval dt, where dW e is the change in electrical energy, dWm is the change in mechanical energy, and dWf is the change in magnetic field energy. Energy losses in the form of heat are neglected.

If the electrical energy is held constant, the dWe term is zero for Equation (1). The differential mechanical energy, in the form of work, is the force multiplied by the differential distance moved. The force due to the magnetic field energy is shown in Equation (2). The negative sign implies that the force is in a direction to decrease the reluctance by making the air gap smaller.

An expression for the energy stored in the magnetic field can be found in terms of the magnetic system parameters. This expression is then substituted into Equation
(2) for Wf to get an expression for the force. This derivation is shown in Appendix A. The result is Equation (3), in terms of the current, i, the constant for the permeability of free space, m0, the cross-sectional area of the air gap, Ag, the number of turns, N, and the air gap distance, x .

To verify this relationship in the lab, it is convenient to have an expression for the current necessary to hold some constant force. In a design, the dimensions and force are often known. So, the user of the reluctance machine needs to know how much current to supply. Rearranging terms in Equation (3) yields Equation (4).

2. Sample Calculations
For the simple magnetic system of Figure 1, the current necessary to suspend the armature can be calculated using Equation (4).
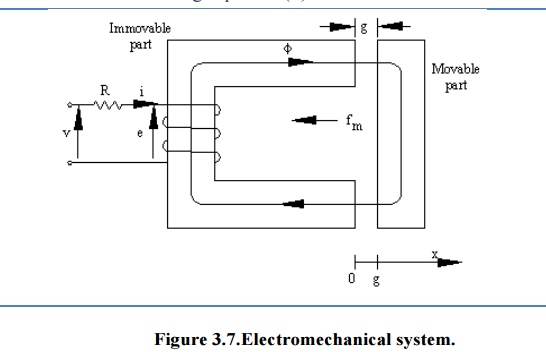
For an air gap length of 0.12 mm, an air gap cross sectional area of 1092 mm 2, and a 230 turn coil the current required to just suspend the 12.5 newton armature is
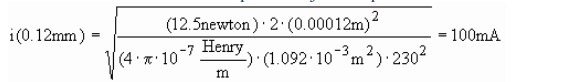
3. Derivation of Magnetic Field Energy and Magnetic Force

Related Topics