Chapter: Mathematics (maths) : Applications of Partial Differential Equations
Solution of LaplaceŌĆÖs equation (Two dimensional heat equation)
Solution of LaplaceŌĆÖs equation (Two dimensional heat equation)
The Laplace equation is
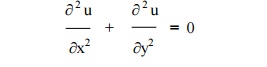
Let u = X(x) . Y(y) be the solution of (1), where ŌĆ×XŌƤ is a function of ŌĆ×xŌƤ alone and ŌĆ×YŌƤ is a function of ŌĆ×yŌƤ alone.
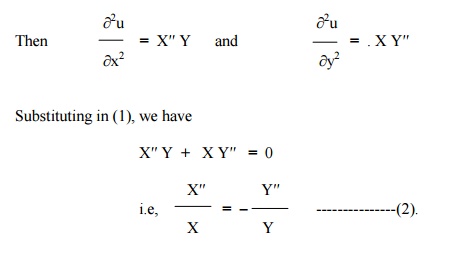
Now the left side of (2) is a function of ŌĆ×xŌƤ alone and the right side is a function of ŌĆ×tŌƤ alone. Since ŌĆ×xŌƤ and ŌĆ×tŌƤ are independent variables, (2) can be true only if each side is equal to a constant.
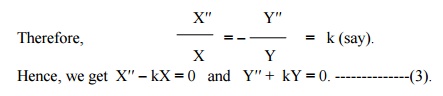
Solving equations (3), we get
(i) when ŌĆ×kŌƤ is positive and k = l2, say
X = c1 elx + c2 e - lx
Y = c3 cosly + c4 sin ly
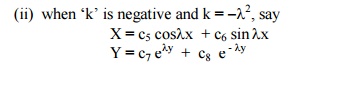
(iii) when ŌĆ×kŌƤ is zero.
X = c9 x + c10
Y = c11 x + c12
Thus the various possible solutions of (1) are
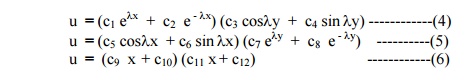
Of these three solutions, we have to choose that solution which suits the physical nature of the problem and the given boundary conditions.
Example 12
An infinitely long uniform plate is bounded by two parallel edges x = 0 & x = Ōäō and an end at right angles to them. The breadth of this edge y = 0 is Ōäō and this edge is maintained at a temperature f (x). All the other 3 edges are at temperature zero. Find the steady state temperature at any interior point of the plate.
Solution
Let u (x,y) be the temperature at any point x,y of the plate.
Also u (x,y) satisfies the equation
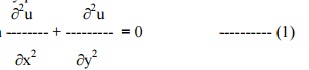


Using (7) in (5), we get the required solution.
Example 13
A rectangular plate with an insulated surface is 8 cm. wide and so long compared to its width that it may be considered as an infinite plate. If the temperature along short edge y = 0 is u(x,0) = 100 sin (px/8), 0 < x < 8, while two long edges x = 0 & x = 8 as well as the other short edges are kept at 0┬░C. Find the steady state temperature at any point of the plate.
Solution
The two dimensional heat equation is given by
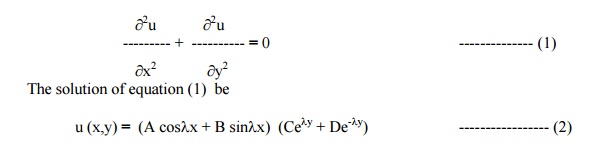
The boundary conditions are
(i) u (0, y) = 0, for 0 < y < ┬ź
(ii) u (8, y) = 0, for 0 < y < ┬ź
(iii) u (x, ┬ź) = 0, for 0 < x < 8
(iv) u (x, 0) = 100 Sin (┬źx/8,) for 0 < x < 8
Using conditions (i), & (ii), we get

Comparing like coefficients on both sides, we get
D1 = 100, D2 = D3 = . . . . = 0
Substituting in (4), we get
u (x,y) = 100 e(-py / 8) sin (px / 8)
Example 14
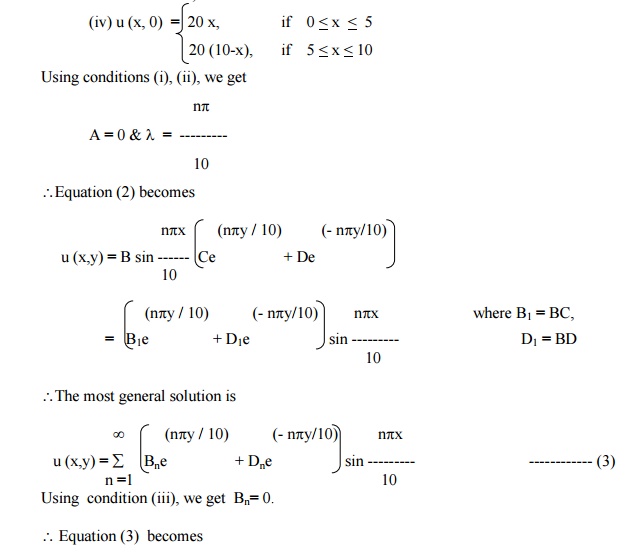
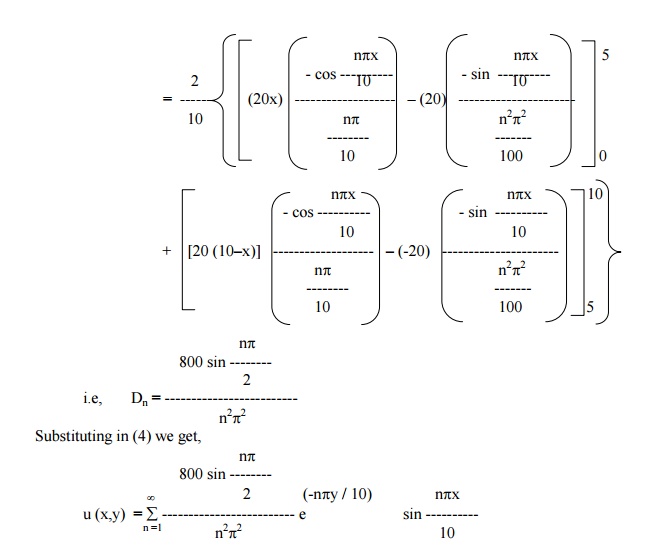
A rectangular plate with an insulated surface 10 c.m wide & so long compared to its width that it may considered as an infinite plate. If the temperature at the short edge y = 0 is given by
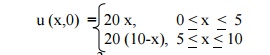
and all the other 3 edges are kept at temperature 0┬░C. Find the steady state temperature at any point of the plate.
Solution
The temperature function u (x,y) is given by the equation
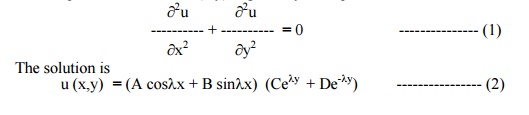
The boundary conditions are
(i) u (0, y) = 0, for 0 < y < ┬ź
(ii) u (10, y) = 0, for 0 < y < ┬ź
(iii) u (x, ┬ź) = 0, for 0 < x < 10

Example 15
A rectangular plate is bounded by the lines x = 0, x = a, y = 0 & y = b. The edge temperatures are u (0,y) = 0, u (x,b) = 0, u (a,y) = 0 & u (x,0) = 5 sin (5px / a) + 3 sin (3px / a). Find the steady state temperature distribution at any point of the plate.
The temperature function u (x,y) satisfies the equation
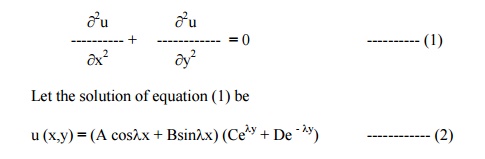
The boundary conditions are
(i) u (0,y) = 0, for 0 < y < b
(ii) u (a,y) = 0, for 0 < y < b
(iii) u (x, b) = 0, for 0 < x < a
(iv) u (x,0) = 5 sin (5px / a) + 3 sin (3px / a), for 0 < x < a.



Exercises
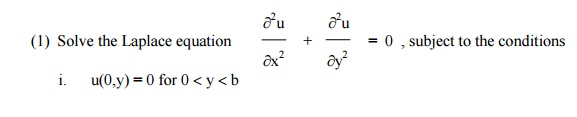
ii. u(a,y) = 0 for 0 <y <b
iii. u(x,b) = 0 for 0 <x <a
iv. u(x,0) = sin3(px/ a) ,0 <x <a.
(2) Find the steady temperature distribution at points in a rectangular plate with insulated faces and the edges of the plate being the lines x = 0, x = a, y = 0 and y = b. When three of the edges are kept at temperature zero and the fourth at a fixed temperature ao C.

i. u(0,y) = 0, 0 ┬Ży ┬Żl ii. u(l,y) = 0, 0 ┬Ży ┬Żl
iii. u(x,0) = 0, 0 ┬Żx ┬Żl iv. u(x,l) = f(x), 0 ┬Żx ┬Żl
(6) A square plate is bounded by the lines x = 0, y = 0, x = 20 and y = 20. Its faces are insulated.
The temperature along the upper horizontal edge is given by u(x,0) = x (20 ŌĆōx), when 0 < x <20,
while other three edges are kept at 0o C. Find the steady state temperature in the plate.
(7) An infinite long plate is bounded plate by two parallel edges and an end at right
angles to them.The breadth is p. This end is maintained0ŌƤatat a c all points and the other edges are at zero temperature. Find the steady state temperature at
any point (x,y) of the plate.
(8) An infinitely long uniform plate is bounded by two parallel edges x = 0 and x = l, and
an end at right angles to them. The breadth of this edge y = 0 is ŌĆ×lŌƤ and temperature f(x). All the other three edges are at temperature zero. Find the steady state
temperature at any interior point of the plate.
(9) A rectangular plate with insulated surface is 8 cm. wide and so long compared to its width that it may be considered infinite in length without introducing an appreciable error. If the temperature along one short edge y = 0 is given by u(x,0) = 100 sin(px/ 8), 0 <x <8, while the two long edges x = 0 and x = 8 as well as the other short edge are kept at 0o C, show that the steady state temperature at any point of the plane is given by u(x,y) = 100 e-py/ 8 sin px/ 8 .
(10) A rectangular plate with insulated surface is 10 cm. wide and so long compared to its width that it may be considered infinite length. If the temperature along short edge y = 0 is given
u(x,0) = 8 sin(px/ 10) when 0 <x <10, while the two long edges x = 0 and x = 10 as well as the other short edge are kept at 0o C, find the steady state temperature distribution u(x,y).
Related Topics