Set Language | Maths - Set Operations | 9th Maths : UNIT 1 : Set Language
Chapter: 9th Maths : UNIT 1 : Set Language
Set Operations
Set Operations
We started with numbers and very soon we learned arithmetical operations on them. In algebra we learnt expressions and soon started adding and multiplying them as well, writing (x2+2) (x-3) etc. Now that we know sets, the natural question is, what can we do with sets, what are natural operations on them ?
What can we do with sets ? We can pick an element. But then which element ? There are many in general, and hence ŌĆ£picking an elementŌĆØ is not an operation on a set. But like we did with addition, subtraction etc, we can try and think of operations that combine two given sets to get a new set. How can we do this ?
A simple way is to put the two sets together. This gives us a new set, and exactly one set, so it is an operation. We could pick out exactly the common elements of the two given sets. ThatŌĆÖs an interesting operation too. We could talk of all the elements not in the given set. But this is problematic: we can list the elements in a set, but which are the elements not in it ? Almost anything. We know that 5734 is in the set of natural numbers, but we also know that my chair is not in it, an elephant is not in it, and so on. How could we ever hope to describe all these elements ? But then when we speak of sets of numbers we are clearly not talking of elephants ! So we should really speak of numbers not in the set of natural numbers. For instance we could implicitly fix the integers and talk of integers not in the set of natural numbers. In general, we call this ŌĆ£fixedŌĆØ set the universal set (relative to which we speak of what is or not in a given set).
When two or more sets combine together to form one set under the given conditions, then operations on sets can be carried out. We can visualize the relationship between sets and set operations using Venn diagram.
John Venn was an English mathematician. He invented Venn diagrams which pictorially represent the relations between sets. Venn diagrams are used in the field of Set Theory, Probability, Statistics, Logic and Computer Science.
1. Universal Set
A Universal set is a set which contains all the elements of all the sets under consideration and is usually denoted by U.
For example,
i. If we discuss about elements in Natural numbers, then the universal set U is the set of all Natural numbers. U={x : x Ōłł N}.
ii. If A={earth, mars, jupiter}, then the universal set U is the planets of solar system.
2. Complement of a Set
The Complement of a set A is the set of all elements of U (the universal set) that are not in A.
It is denoted by AŌĆ▓ or Ac. In symbols AŌĆ▓= {x : xŌłłU, xŌłēA}
Venn diagram for complement of a set
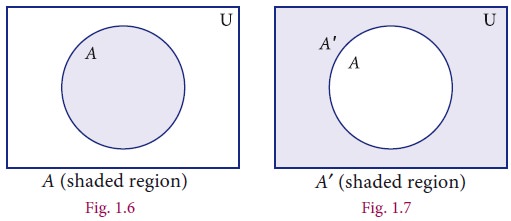
For example,
If U = {all boys in a class} and A= {boys who play Cricket}, then complement of the set A is AŌĆ▓= {boys who do not play Cricket}.
Example 1.9
If U = {c, d, e, f, g, h, i, j} and A = { c, d, g, j} , find AŌĆ▓.
Solution
U = {c, d, e, f, g, h, i, j}, A = {c, d, g, j}
AŌĆ▓ ={e, f, h, i}

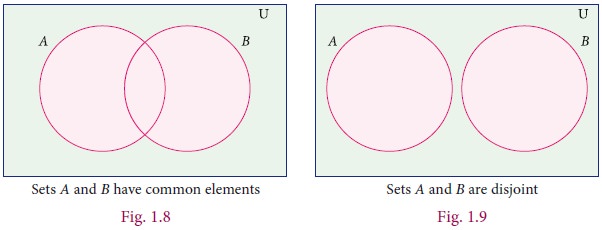
3. Union of Two Sets
The union of two sets A and B is the set of all elements which are either in A or in B or in both. It is denoted by AŌł¬B and read as A union B.
In symbol, AŌł¬B = {x : x ŌłłA or xŌłłB}
The union of two sets can be represented by Venn diagram as given below
For example,
If P ={Asia,Africa, Antarctica, Australia} and Q = {Europe, North America, South America}, then the union set of P and Q is PŌł¬Q = {Asia, Africa, Antartica, Australia, Europe, North America, South America}.

Example 1.10
If A={1, 2, 6} and B={2, 3, 4} , find AŌł¬B.
Solution
Given A={1, 2, 6}, B={2, 3, 4}
AŌł¬B={1, 2, 3, 4,6}.
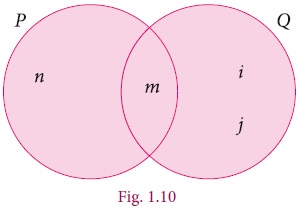
Example 1.11
If P={m, n} and Q= {m, i, j}, represent P and Q in Venn diagram and find PŌł¬Q.
Solution
Given P={m, n} and Q= {m, i, j}
From the diagram,
PŌł¬Q={n, m, i, j}.
4. Intersection of Two Sets
The intersection of two sets A and B is the set of all elements common to both A and B. It is denoted by AŌł®B and read as A intersection B.
In symbol , AŌł®B={x : xŌłłA and xŌłłB}
Intersection of two sets can be represented by a Venn diagram as given below
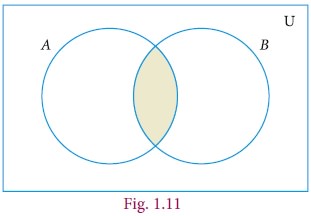
For example,
If A = {1, 2, 6}; B = {2, 3, 4}, then AŌł®B = {2} because 2 is common element of the sets A and B.

Can we determine n(A Ōł® B) in terms of n(A) and n(B)? This seems to be difficult, but what about n(A Ōł¬ B) in terms of n(A) and n(B) ?
Notice that all the elements in A are in (A Ōł¬ B), and all the elements in B also in A Ōł¬ B
Can we say that n(A Ōł¬ B) = n(A) + n(B) ?
Unfortunately not. Consider an element is common to both A and B? Of course it is in A union B, but is counted both in A and in B and we donŌĆÖt want to count the same element twice in A union B !
So indeed, n(A Ōł¬ B) = n(A) + n(B) ŌĆō n(A Ōł® B). But then it is easy to see that n(A Ōł®B) = n(A) + n(B) ŌĆō n(A Ōł¬ B). So between the union and the intersection we need to know one to determine the other, given n(A) and n(B).
Example 1.12
Let A = {x : x is an even natural number and 1< x Ōēż 12} and
B = { x : x is a multiple of 3, x Ōłł N and xŌēż12} be two sets. Find AŌł®B.
Solution
Here A = {2, 4, 6, 8, 10, 12} and B = {3, 6, 9, 12}
AŌł®B = {6, 12}
Example 1.13
If A = {2, 3} and C = { }, find AŌł®C.
Solution
There is no common element and hence AŌł®C ={ }
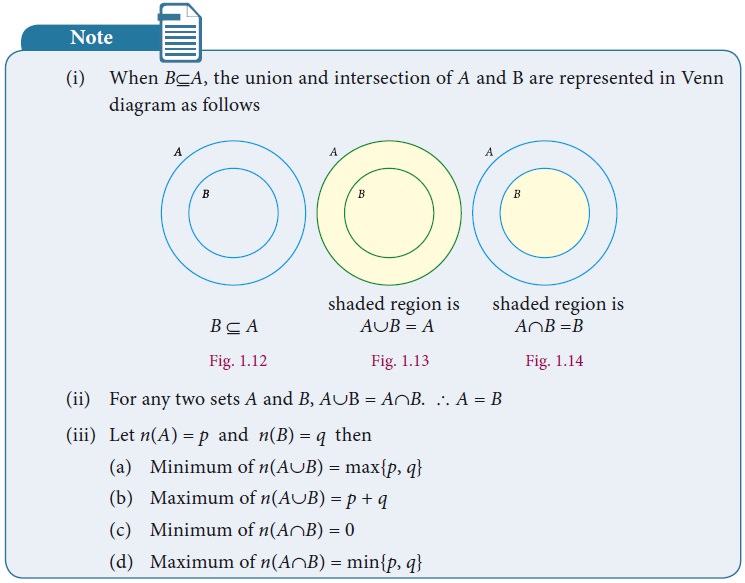
5. Difference of Two Sets
Let A and B be two sets, the difference of sets A and B is the set of all elements which are in A, but not in B. It is denoted by AŌĆōB or A\B and read as A difference B.
In symbol, AŌĆōB = { x : x Ōłł A and x Ōłē B}
BŌĆōA = { y : y Ōłł B and y Ōłē A}.
Venn diagram for set difference
Example 1.14
If A={ŌĆō3, ŌĆō2, 1, 4} and B= {0, 1, 2, 4}, find (i) AŌĆōB (ii) BŌĆōA.
Solution
AŌĆōB ={ŌĆō3, -2, 1, 4} ŌĆō {0, 1, 2, 4} = { -3, -2}
BŌĆōA = {0, 1, 2, 4} ŌĆō{ŌĆō3, -2, 1, 4} = { 0, 2}

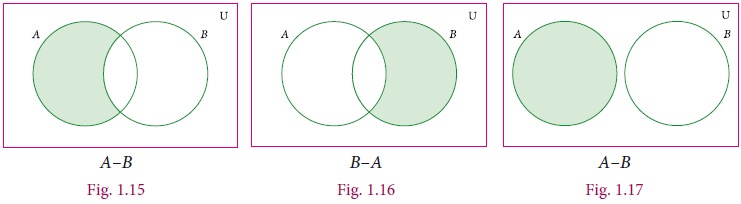
6. Symmetric Difference of Sets
The symmetric difference of two sets A and B is the set (AŌĆōB)Ōł¬(BŌĆōA). It is denoted by A╬öB.
A B={ x : x Ōłł AŌĆōB or x Ōłł BŌĆōA}
Example 1.15
If A = {6, 7, 8, 9} and B={8, 10, 12}, find AΔB.
Solution
AŌĆōB = {6, 7, 9}
BŌĆōA = {10, 12}
A╬öB = (AŌĆōB)Ōł¬(BŌĆōA) = {6, 7, 9}Ōł¬{10,12}
AΔB = {6, 7, 9, 10, 12}.
Example 1.16
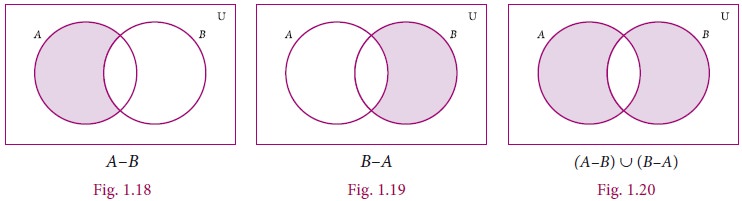
Represent AΔB through Venn diagram.
Solution
A╬öB= (AŌĆōB) Ōł¬ (BŌĆōA)

7. Disjoint Sets
Two sets A and B are said to be disjoint if they do not have common elements.
In other words, if AŌł®B=Ōłģ, then A and B are said to be disjoint sets.
Example 1.17
Verify whether A={20, 22, 23, 24} and B={25, 30, 40, 45} are disjoint sets.
Solution
A = {20,22, 23, 24} , B={25, 30, 40, 45}
AŌł®B = {20,22, 23, 24} Ōł® {25, 30, 40, 45}
= { }
Since AŌł®B = Ōłģ, A and B are disjoint sets.

Example 1.18
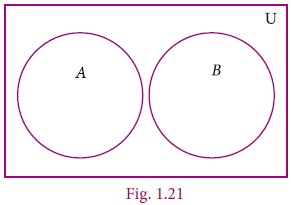
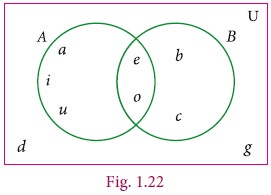
From the given Venn diagram, write the elements of
(i) A (ii) B (iii) AŌĆōB (iv) BŌĆōA (v) AŌĆ▓ (vi) BŌĆ▓ (vii) U
Solution
(i) A = {a, e, i, o, u}
(ii) B = {b, c, e, o}
(iii) AŌĆōB = {a, i, u}
(iv) BŌĆōA = {b, c}
(v) AŌĆ▓ = {b, c, d, g}
(vi) BŌĆ▓ = {a, d, g, i, u}
(vii) U = {a, b, c, d, e, g, i, o, u}
Example 1.19
Draw a Venn diagram similar to one at the side and shade the region representing the following sets
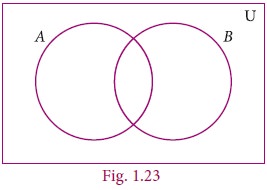
(i) AŌĆ▓ (ii) (AŌĆōB)ŌĆ▓ (iii) (AŌł¬B)ŌĆ▓
Solution
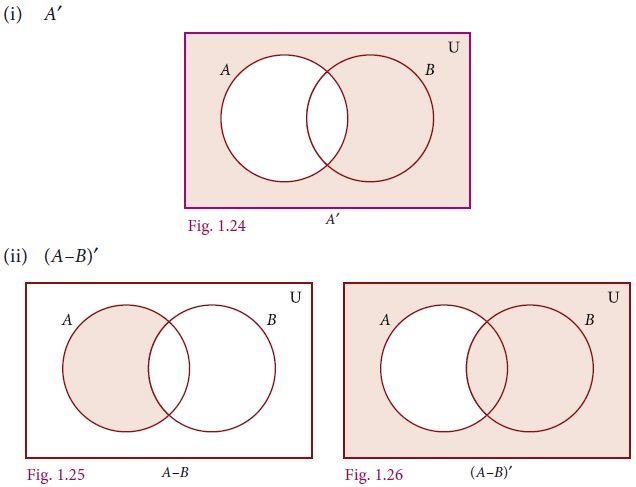
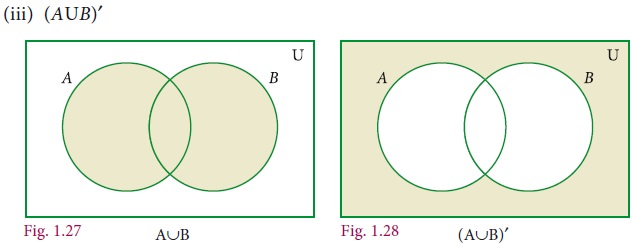
Related Topics