Numerical Problems with Answers, Solution | Set Language | Maths - Exercise 1.5: De MorganŌĆÖs Laws | 9th Maths : UNIT 1 : Set Language
Chapter: 9th Maths : UNIT 1 : Set Language
Exercise 1.5: De MorganŌĆÖs Laws
Exercise 1.5
1. Using the adjacent Venn diagram, find
the following sets:
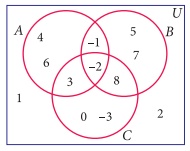
(i) A ŌłÆ B (ii) B -C (iii) AŌĆ▓ Ōł¬ BŌĆ▓ (iv) AŌĆ▓ Ōł® BŌĆ▓ (v) (B Ōł¬C)ŌĆ▓ (vi) A ŌłÆ (B Ōł¬C) (vii) A ŌłÆ (B Ōł®C)

2. If K = { a , b, d, e, f } , L = { b,
c, d, g } and M = { a , b, c, d, h
} , then find the following:
(i) K Ōł¬ (L Ōł® M) (ii) K Ōł® (L Ōł¬ M) (iii) (K Ōł¬ L ) Ōł® (K Ōł¬ M) (iv) (KŌł® L) Ōł¬ (K Ōł® M)
and verify distributive laws.

3. If A = {x : x Ōłł Ōäż, ŌłÆ
2 < x Ōēż 4}, B={x : x Ōłł W , x Ōēż
5}, C = {ŌłÆ4, ŌłÆ1, 0, 2, 3, 4}, then verify
A Ōł¬ (B
Ōł®C ) = (A Ōł¬ B )
Ōł® (A Ōł¬C) .

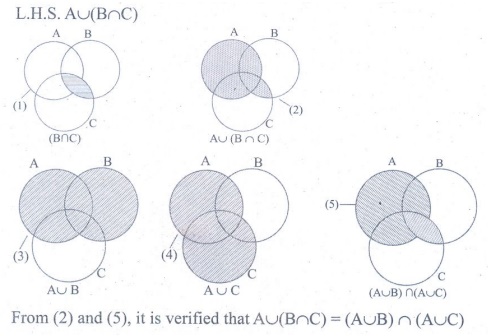
4. Verify A Ōł¬ (B Ōł®C ) = (A Ōł¬ B ) Ōł® (A Ōł¬C) using Venn diagrams.
5. If A = {b, c,
e, g, h} , B = {a , c, d , g,
i } and C = {a , d, e, g, h} ,
then show that AŌłÆ(B Ōł®C)
= (AŌłÆB)Ōł¬(AŌłÆC).
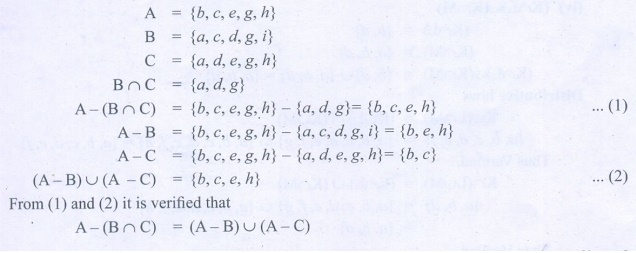
6. If A = {x : x
= 6n, nŌłłW and n<6}, B = {x
: x = 2n, n Ōłł ŌäĢ and 2<nŌēż9} and C = {x
: x = 3n, n Ōłł ŌäĢ and 4Ōēżn<10},
then show that A ŌłÆ (B Ōł®
C ) = (A ŌłÆ
B ) Ōł¬
(A ŌłÆC)


7. If A = {ŌĆō2,0,1,3,5}, B
= {ŌĆō1,0,2,5,6} and C = {ŌĆō1,2,5,6,7}, then show that A ŌłÆ (B
Ōł¬C) =
(AŌłÆB)Ōł®(AŌłÆC).

8. If A = {y : y = [a + 1] /2 , aŌłłW and a Ōēż 5}, B = {y : y = [2n -1] / 2, nŌłłW and n < 5} and C = {-1, -1/2,1,3/2,2},
then show that A ŌłÆ (B Ōł¬ C )
= (A ŌłÆ B ) Ōł® (A ŌłÆC) .
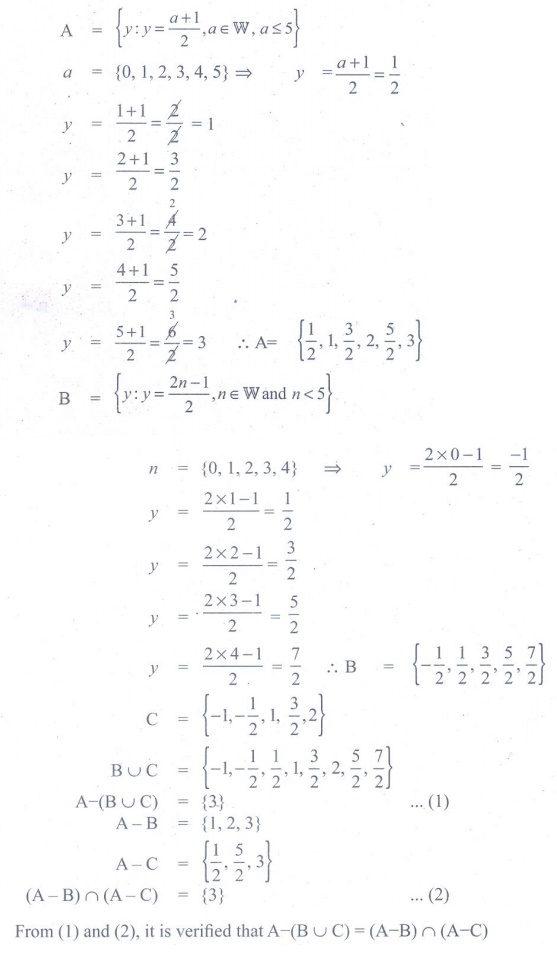
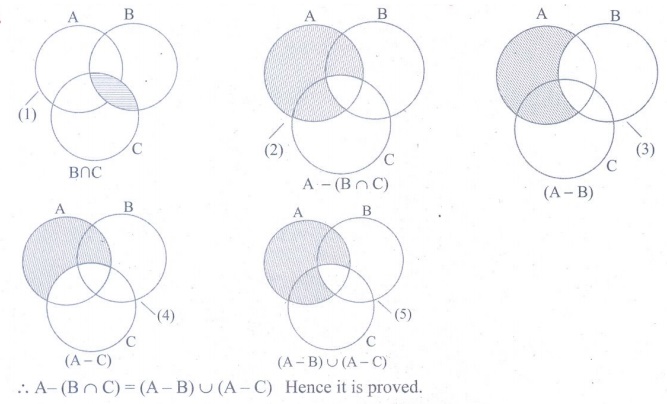
9. Verify A ŌłÆ (B
Ōł® C
) = (A ŌłÆ B
) Ōł¬ (A
ŌłÆC) using
Venn diagrams.
10. If U = {4,7,8,10,11,12,15,16},
A={7,8,11,12} and B = {4,8,12,15} then verify De MorganŌĆÖs Laws for
complementation.

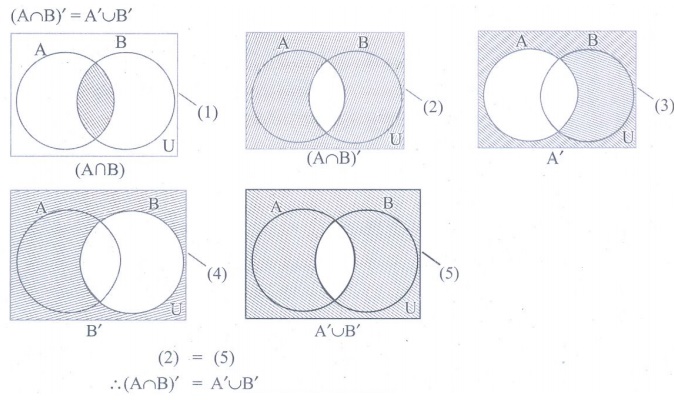
11. Verify (A Ōł® B)ŌĆ▓ = AŌĆ▓ Ōł¬ BŌĆ▓ using Venn diagrams.
Related Topics