Definition, Example Solved Problems | Set Language | Maths - De MorganŌĆÖs Laws | 9th Maths : UNIT 1 : Set Language
Chapter: 9th Maths : UNIT 1 : Set Language
De MorganŌĆÖs Laws
De MorganŌĆÖs Laws
Augustus
De Morgan (1806 ŌĆō 1871) was a British mathematician. He was born on 27th
June 1806 in Madurai, Tamilnadu, India. His father was posted in India by the East
India Company. When he was seven months old, his family moved back to England. De
Morgan was educated at Trinity College, Cambridge, London. He formulated laws for
set difference and complementation. These are called De MorganŌĆÖs laws.
1. De MorganŌĆÖs Laws for Set Difference
These
laws relate the set operations union, intersection and set difference.
Let
us consider three sets A, B and C as A = {ŌłÆ5, ŌłÆ2,1, 3}, B =
{ŌłÆ3,ŌłÆ2,
0, 3, 5}
and C = {ŌłÆ2,ŌłÆ1,
0, 4,5}.
Now, B Ōł¬C = {-3,-2,-1,
0, 3, 4,5}
A ŌłÆ (B Ōł¬C) = { ŌłÆ5,1 } ... (1)
Then,
A ŌłÆ B = {-5, 1}
and A ŌłÆ C = { ŌłÆ5, 1, 3}
(AŌłÆB)Ōł¬(AŌłÆC) = { ŌłÆ5,1, 3 } ... (2)
(AŌłÆB)Ōł®(AŌłÆC) =
{ ŌłÆ5,1 } ... (3)
From (1) and (2), we see that
AŌłÆ(B Ōł¬C) ŌēĀ (AŌłÆB)Ōł¬(AŌłÆC)
But note that from (1) and (3), we see that
AŌłÆ(B Ōł¬C) =
(AŌłÆB)Ōł®(AŌłÆC)
Thinking Corner
(AŌłÆB) Ōł¬(AŌłÆC) Ōł¬(A Ōł® B)=____
Now, B Ōł®C = {
ŌłÆ2, 0, 5 }
AŌłÆ(B Ōł®C) = { ŌłÆ5,1, 3 } ... (4)
From (3)
and (4) we see that
AŌłÆ(B Ōł®C) ŌēĀ
(AŌłÆB)Ōł®(AŌłÆC)
But
note that from (2) and (4), we get A ŌłÆ (B Ōł®
C ) = (A ŌłÆ B ) Ōł¬ (A ŌłÆC)
De MorganŌĆÖs laws for set difference : For any three sets A,
B and C
(i) A ŌłÆ (B Ōł¬ C ) = (A ŌłÆ B ) Ōł® (A ŌłÆC) (ii) A ŌłÆ (B Ōł® C ) = (A ŌłÆ B ) Ōł¬ (A ŌłÆC)
Example 1.23
Verify
A ŌłÆ (B Ōł¬
C ) = (A ŌłÆ B ) Ōł®
(A ŌłÆC) using Venn diagrams.
Solution
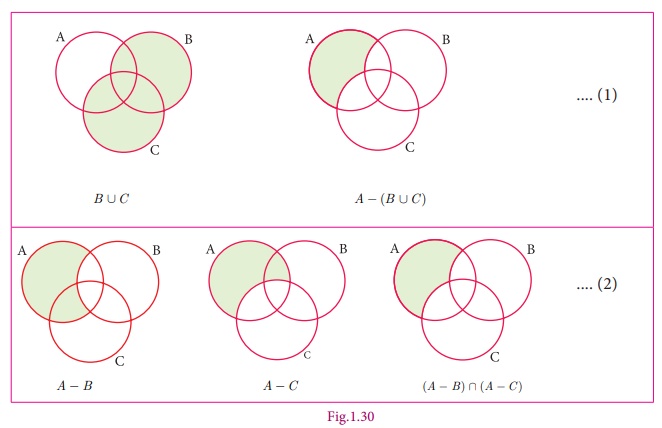
From
(1) and (2), we get A ŌłÆ (B Ōł¬C ) = (A ŌłÆ
B ) Ōł® (A ŌłÆC) . Hence it is verified.
Example 1.24
If
P = {x : xŌłł
W and 0 < x < 10}, Q
= {x : x = 2n+1, nŌłł
W and n<5} and R =
{ 2, 3, 5, 7,11, 13}, then verify P ŌłÆ (Q Ōł®
R ) = (P ŌłÆQ ) Ōł¬
(P ŌłÆ R)
Solution The roster form of sets P, Q and R are
P
=
{1,2,3,4,5,6,7,8,9} , Q = {1,3,5,7,9} and R = {2, 3, 5, 7,11, 13}
First, we find (Q Ōł® R) = { 3,5,7 }
Then, P ŌłÆ (Q Ōł® R) = { 1,2,4,6,8,9 } ... (1)
Next, PŌĆōQ = { 2,4,6,8 } and
PŌĆōR = { 1,4,6,8,9 }
and so, (P ŌłÆ Q) Ōł¬ (P ŌłÆ R) =
{ 1,2, 4,6, 8,9} ... (2)
Hence
from (1) and (2), it is verified that P ŌłÆ (Q Ōł®
R ) = (P ŌłÆQ ) Ōł¬
(P ŌłÆ R).
Finding the elements of
set Q
Given, x = 2n + 1
n = 0 ŌåÆ x = 2(0) +1 = 0 +1 = 1
n = 1 ŌåÆ x = 2(1) +1 = 2 +1 = 3
n = 2 ŌåÆ x = 2(2) +1 = 4 +1 = 5
n = 3 ŌåÆ x = 2(3) +1 = 6 +1 = 7
n = 4 ŌåÆ x = 2(4) +1 = 8 +1 = 9
Therefore, x takes values such as 1, 3, 5, 7 and 9.
2. De MorganŌĆÖs Laws for Complementation
These
laws relate the set operations on union, intersection and complementation.
Thinking Corner : Check whether AŌłÆB =AŌł®BŌĆ▓
Let
us consider universal set U={0,1,2,3,4,5,6}, A={1,3,5} and B={0,3,4,5}.
Now, A Ōł¬ B = {0,1,
3, 4,5}
Then, (A Ōł¬ B)ŌĆ▓ = {2,6}
.....(1)
Next, AŌĆ▓ =
{0, 2, 4, 6} and BŌĆ▓ = {1,2,6}
Then, AŌĆ▓ Ōł® BŌĆ▓ = {2,6} .....(2)
From (1) and (2), we get (A Ōł¬ B)ŌĆ▓ = AŌĆ▓ Ōł® BŌĆ▓
Also, A Ōł® B = {3, 5},
Thinking Corner (AŌłÆ B) Ōł¬ (B ŌłÆ AŌĆ▓ ) = ____
(A Ōł® B)ŌĆ▓ = {0,1,2,
4, 6} .....(3)
AŌĆ▓ = { 0,2,4,6 } and BŌĆ▓ = { 1,2,6 }
AŌĆ▓ Ōł¬ BŌĆ▓ = { 0,1,2,
4,6 } .....(4)
From
(3) and (4), we get (A Ōł® B)ŌĆ▓
=
AŌĆ▓
Ōł¬ BŌĆ▓
De MorganŌĆÖs laws for complementation : Let ŌĆśUŌĆÖ be the universal
set containing finite sets A and B. Then (i) (A Ōł¬ B)ŌĆ▓ = AŌĆ▓ Ōł® BŌĆ▓ (ii) (A Ōł® B)ŌĆ▓ = AŌĆ▓ Ōł¬ BŌĆ▓
Example 1.25
Verify
(A Ōł¬ B)ŌĆ▓
=
AŌĆ▓ Ōł®
BŌĆ▓
using Venn diagrams.
Solution

From
(1) and (2), it is verified that (A Ōł¬ B)ŌĆ▓
=
AŌĆ▓ Ōł®
BŌĆ▓
Example 1.26
If
U = {x : x Ōłł
Ōäż, ŌłÆ 2 Ōēż x Ōēż
10},
A = {x : x =
2 p +
1, p Ōłł Ōäż, ŌłÆ 1 Ōēż p Ōēż
4}, B =
{x
: x =
3q +
1, q Ōłł Ōäż, ŌłÆ 1 Ōēż q <
4}, verify De MorganŌĆÖs laws for complementation.
Solution
Given
U = {ŌłÆ2, ŌłÆ1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
,
A= {ŌłÆ1, 1, 3, 5, 7, 9} and B = {ŌłÆ2,
1, 4, 7,10}
Thinking Corner A Ōł® (A Ōł¬ B)ŌĆ▓ =____
Law (i) (A Ōł¬ B)ŌĆ▓ = AŌĆ▓ Ōł® BŌĆ▓
Now, A Ōł¬ B = {-2,-1,1,
3, 4,5,7,9,10}
(A Ōł¬ B)ŌĆ▓ = {0,2,6, 8} ..... (1)
Then, AŌĆ▓ =
{-2, 0, 2, 4, 6, 8,10} and BŌĆ▓ = {-1, 0,2, 3,5,6, 8,9}
AŌĆ▓ Ōł® BŌĆ▓ = {0,
2, 6, 8} ..... (2)
From (1) and (2), it is verified that (AŌł¬B)ŌĆ▓ = AŌĆ▓ Ōł® B ŌĆ▓
Law (ii) (A Ōł® B)ŌĆ▓ =AŌĆ▓ Ōł¬BŌĆ▓
Now, A Ōł® B = {1,7}
(A Ōł® B)ŌĆ▓ = {-2,-1,
0,2, 3, 4,5,6, 8,9,10} ..... (3)
Then, AŌĆ▓ Ōł¬ BŌĆ▓ = {-2,-1,
0,2, 3, 4,5,6, 8,9,10} .....
(4)
From (3) and (4), it is verified that (AŌł®B)ŌĆ▓ = AŌĆ▓ Ōł¬ BŌĆ▓
Thinking Corner (A Ōł¬ B)ŌĆ▓ Ōł¬ (AŌĆ▓ Ōł® B) =___
Related Topics