with Answers, Solution | Set Language | Maths - Exercise 1.7: Multiple Choice Questions | 9th Maths : UNIT 1 : Set Language
Chapter: 9th Maths : UNIT 1 : Set Language
Exercise 1.7: Multiple Choice Questions
Exercise 1.7
Multiple Choice Questions
1. Which of the following is correct?
(1) {7} Ōłł {1,2,3,4,5,6,7,8,9,10}
(2) 7 Ōłł {1,2,3,4,5,6,7,8,9,10}
(3) 7 Ōłē {1,2,3,4,5,6,7,8,9,10}
(4) {7} ŌŖł {1,2,3,4,5,6,7,8,9,10}
[Answer:
(2)]
2. The set P = {x | x Ōłł Ōäż , ŌĆō1< x < 1} is a
(1) Singleton set
(2) Power set
(3) Null set
(4) Subset
Solution: P = {0}
[Answer: (1) Singleton set]
3. If U ={x | x Ōłł ŌäĢ, x < 10} and A = {x | x Ōłł ŌäĢ, 2 Ōēż x < 6} then (AŌĆ▓)ŌĆ▓ is
(1) {1, 6, 7, 8, 9}
(2) {1, 2, 3, 4}
(3) {2, 3, 4, 5}
(4) { }
Solution: (A') = A= {2, 3,4, 5}
[Answer: (3) {2, 3,4, 5}]
4. If BŌŖå A then n(AŌł®B) is
(1) n(AŌĆōB)
(2) n(B)
(3) n(B ŌĆō A)
(4) n(A)
Solution: B ŌŖå A ŌćÆ AŌł®B = B
[Answer: (2)]
5. If A = {x, y, z} then the number of non- empty subsets of A is
(1) 8
(2) 5
(3) 6
(4) 7
Solution: Number of non-empty subsets =2-1=8-1=7
[Answer:(4) 7]
6. Which of the following is correct?
(1) Ōłģ ŌŖå {a, b}
(2) Ōłģ Ōłł {a, b}
(3) {a} Ōłł {a, b}
(4) a ŌŖå {a, b}
Solution: Empty set is an improper subset
[Answer: (1)]
7. If AŌł¬B = AŌł®B, then
(1) AŌēĀB
(2) A = B
(3) A ŌŖé B
(4)BŌŖéA
[Answer:
(2) A=B ]
8. If B ŌĆō A is B, then AŌł®B is
(1) A
(2) B
(3) U
(4) Ōłģ
Solution: B - A = B ŌćÆ A and B are disjoint
sets.
[Answer: (4)]
9. From the adjacent diagram n[P(AŌłåB)] is
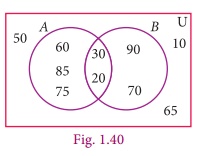
(1) 8
(2) 16
(3) 32
(4) 64
Solution: A Δ B = { 60, 85, 75, 90, 70}
ŌćÆ n(A ╬ö B) = 5
ŌćÆ n(P (A ╬ö B)) = 25 = 32
[Answer: (3) 32]
10. If n(A) = 10 and n(B) = 15, then the minimum and maximum number of elements in A Ōł® B is
(1) 10,15
(2) 15,10
(3) 10,0
(4) 0,10
[Answer: (4)
(0,10) ]
11. Let A = {Ōłģ} and B = P(A), then AŌł®B is
(1) {Ōłģ,{Ōłģ}}
(2) {Ōłģ}
(3) Ōłģ
(4) {0}
Solution: P(A) = { ├ś{├ś}}
[Answer: (2) { ├ś } ]
12. In a class of 50 boys, 35 boys play Carrom and 20 boys play Chess then the number of boys play both games is
(1) 5
(2) 30
(3) 15
(4) 10.
Solution: n(AŌł¬B) = n(A) + n(B) ŌĆö n(AŌł®B) ŌćÆ 50 = 35 + 20 ŌĆö n(AŌł®B) ŌćÆ n(AŌł®B) = 5
[Answer: (1) 5]
13. If U = {x : x Ōłł ŌäĢ and x < 10} , A = { 1,2,3,5,8 } and B = { 2,5,6,7,9 }, then n [(A Ōł¬ B)ŌĆ▓] is
(1) 1
(2) 2
(3) 4
(4) 8
Solution: U = {1, 2, 3,4, 5, 6, 7, 8, 9}
A = {1,2, 3, 5, 8}
B = {2, 5, 6, 7, 9}
AŌł¬B = {1,2, 3,5, 6, 7, 8, 9}
(AŌł¬B)' = {4},
n(AŌł¬B)' = 1
[Answer:
(1) 1]
14. For any three sets P, Q and R, P ŌłÆ (Q Ōł® R) is
(1) P ŌłÆ(Q Ōł¬R)
(2) (P Ōł®Q)ŌłÆR
(3) (P ŌłÆQ)Ōł¬(P ŌłÆR)
(4) (P ŌłÆQ)Ōł®(P ŌłÆR)
Solution: P-(QŌł®R) = (P-Q)Ōł¬(P-R)
[Answer: (3) (P-Q)Ōł¬(P-R)]
15. Which of the following is true?
(1) AŌłÆB =AŌł®B
(2) AŌłÆB=BŌłÆA
(3) (AŌł¬B)ŌĆ▓ =AŌĆ▓ Ōł¬BŌĆ▓
(4) (AŌł®B)ŌĆ▓ =AŌĆ▓ Ōł¬BŌĆ▓
Solution :
(1) (A-B) = AŌł®B False
(2) A-B = B-A False
(3) (AŌł¬B)' = A' Ōł¬ B' False
(4) (AŌł®B)' = A' Ōł¬ B' True
[Answer: (4) (AŌł®B)' = A' Ōł¬ B']
16. If n (A Ōł¬ B Ōł¬C) = 100, n (A) = 4x, n (B) = 6x, n (C ) = 5x, n (A Ōł® B) = 20, n (B Ōł® C) = 15, n (A Ōł® C) = 25 and n(A Ōł® B Ōł®C) = 10 , then the value of x is
(1) 10
(2) 15
(3) 25
(4) 30
Solution:
n(AŌł¬BŌł¬C) = n(A) + n(B) + n(C) - n(AŌł®B) - n(BŌł®C) - n(CŌł®A) + n(AŌł®BŌł®C)
100 = 4x + 6x
+ 5x - 20 ŌĆō 15 -25 + 10
100 = 15x-60+10
100 = 15x-50
15x = 100 + 50 = 150
x = 10
[Answer: (1)10]
17. For any three sets A, B and C, (A ŌłÆ B) Ōł® (B ŌłÆC) is equal to
(1) A only
(2) B only
(3) C only
(4) ŽĢ
Solution: (A - B) Ōł® (B - C) is equal to ŽĢ
[Answer: (4) ŽĢ ]
18. If J = Set of three sided shapes, K = Set of shapes with two equal sides and L = Set of shapes with right angle, then J Ōł® K Ōł® L is
(1) Set of isoceles triangles
(2) Set of equilateral triangles
(3) Set of isoceles right triangles
(4) Set of right angled triangles
Solution:
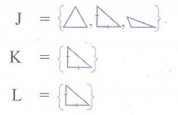
[Answer: (3) Set of isoceles right triangles]
19. The shaded region in the Venn diagram is
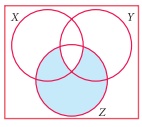
(1) Z ŌłÆ(X Ōł¬Y)
(2) (X Ōł¬Y)Ōł®Z
(3) Z ŌłÆ(X Ōł®Y)
(4) Z Ōł¬(X Ōł®Y)
Solution: Z ŌĆō (X Ōł®Y)
[Answer: (3) Z ŌĆō (X Ōł®Y) ]
20. In a city, 40% people like only one fruit, 35% people like only two fruits, 20% people like all the three fruits. How many percentage of people do not like any one of the above three fruits?
(1) 5
(2) 8
(3) 10
(4) 15
Solution:
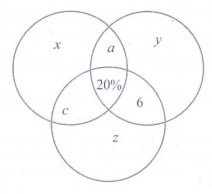
40 + 35 + 20 + x = 100%
95% + x = 100%
x = 5%
[Answer: (1) 5]
Related Topics