Set Language | Maths - Properties of Set Operations | 9th Maths : UNIT 1 : Set Language
Chapter: 9th Maths : UNIT 1 : Set Language
Properties of Set Operations
Properties of Set Operations
It
is an interesting investigation to find out if operations among sets (like union,
intersection, etc) follow mathematical properties such as Commutativity, Associativity,
etc., We have seen numbers having many of these properties; whether sets also possess
these, is to be explored.
We
first take up the properties of set operations on union and intersection.
1. Commutative Property
In
set language, commutative situations can be seen when we perform operations. For example, we can look into the Union (and Intersection)
of sets to find out if the operation is commutative.
Note
For any set A,
ŌĆó A Ōł¬ A = A and A Ōł® A = A [Idempotent Laws].
ŌĆó A Ōł¬ ŽĢ = A and A Ōł® U = A [Identity Laws].
Let A
=
{2,
3, 8,10}
and B = {1, 3,10, 13}
be two sets.
Then, A
Ōł¬ B =
{1,
2, 3, 8,10, 13} and
B
Ōł¬ A =
{1,2,
3, 8,10,13}
From the
above, we see that A Ōł¬
B = B Ōł¬
A.
This is called
Commutative property of union of sets.
Now, A
Ōł®
B = {3, 10} and B Ōł®
A = {3, 10}. Then, we see that A Ōł®
B = B Ōł® A .
This
is called Commutative property of intersection of sets.
Commutative property: For any two sets A and B
(i) A Ōł¬ B =B Ōł¬ A
(ii) A Ōł® B =B Ōł® A
Example 1.19
If A = {b, e, f ,g} and B
= {c, e, g,h}, then verify the commutative
property of (i) union of sets (ii) intersection
of sets.
Solution
Given, A = { b, e, f ,g }
and B = { c, e, g,h }
(i) A Ōł¬ B = { b, c,e, f ,g , h } ... (1)
B Ōł¬ A = { b, c, e, f, g, h } ... (2)
From
(1) and (2) we have A Ōł¬
B = B Ōł¬
A
It
is verified that union of sets is commutative.
(ii) AŌł®B = { e, g } ... (3)
BŌł®A= { e, g } ... (4)
From
(3) and (4) we get, A Ōł® B =
B Ōł® A
It
is verified that intersection of sets is commutative.
Thinking Corner
Given, P = { l, n , p } and P
Ōł¬ Q = { j ,l ,m , n,o , p}. If P and Q are disjoint sets, then what will be Q and P Ōł®Q ?
Note
Recall that subtraction on numbers is not commutative. Is set difference
commutative? We expect that the set difference is not commutative as well. For instance,
consider A = { a , b, c }, B = { b, c, d }. AŌłÆB = { a }, BŌłÆA= { d } ; we see that
A ŌłÆ B ŌēĀ B ŌłÆ A.
2. Associative Property
Now, we perform
operations on union and intersection for three sets.
Let
A = {ŌłÆ 1, 0, 1, 2}, B =
{ŌłÆ3,
0, 2, 3} and C = {0, 1, 3, 4} be three sets.
Now,
B Ōł¬ C = {-3, 0,1,2, 3, 4}
AŌł¬(B Ōł¬C) = {ŌłÆ1, 0,1,2} Ōł¬{ŌłÆ3, 0,1,2, 3, 4}
= {-3,-1, 0,1,2, 3, 4} ... (1)
Then,
A Ōł¬ B = {-3,-1, 0,1,2, 3}
(AŌł¬B)Ōł¬C = {ŌłÆ3,ŌłÆ1, 0,1,2, 3} Ōł¬{0,1, 3, 4}
= {-3,-1, 0,1,2, 3, 4} ... (2)
From
(1) and (2), A Ōł¬
(B Ōł¬C ) = (A Ōł¬ B ) Ōł¬C .
This
is associative property of union among setsA, B, and C.
Now,
B Ōł®C = {0, 3}
AŌł®(B Ōł®C) = {ŌłÆ1, 0,1,2} Ōł®{0, 3}
= {0} ... (3)
Then,
A Ōł® B = {0,2}
(AŌł®B)Ōł®C = {0,2} Ōł® {0,1, 3, 4}
= {0} ... (4)
From
(3) and (4), A Ōł® (B Ōł®C ) = (A Ōł®
B ) Ōł®C .
This
is associative property of intersection among setsA, B and C.
Associative property: For any three sets A, B and C
(i) A Ōł¬ (B Ōł¬C ) = (A Ōł¬ B ) Ōł¬C
(ii) A Ōł® (B Ōł®C ) = (A Ōł® B ) Ōł®C
Example 1.20
If 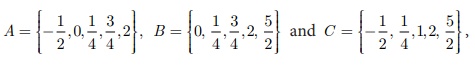 then verify A Ōł® (B Ōł®C ) = (A Ōł®
B ) Ōł®C .
then verify A Ōł® (B Ōł®C ) = (A Ōł®
B ) Ōł®C .
Solution
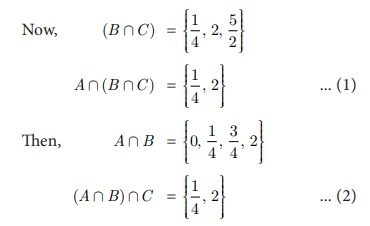
From
(1) and (2), it is verified that
(AŌł®B)Ōł®C = AŌł®(B
Ōł®C)
Note
The set difference in general is not associative
that is, (AŌĆōB)ŌĆōC ŌēĀAŌĆō(BŌĆōC).
But, if the sets A, B and C are mutually disjoint
then the set difference is associative
that is, (AŌĆōB)ŌĆōC=AŌĆō(BŌĆōC).
3. Distributive Property
In
lower classes, we have studied distributive property of multiplication over
addition on numbers. That is, a ├Ś (b +c ) = (a ├Śb ) + (a ├Śc). In the same way we can define
distributive properties on sets.
Distributive property: For any three sets A, B and C
(i) A Ōł® (B Ōł¬C ) = (A Ōł® B ) Ōł¬ (A Ōł®C) [Intersection over union]
(ii) A Ōł¬ (B Ōł®C ) = (A Ōł¬ B ) Ōł® (A Ōł¬C) [Union over intersection]
Example 1.21
If
A = {0, 2, 4, 6, 8},
B = {x : x is a prime number and x < 11}
and C= {x : x Ōłł
N and 5 Ōēż x <
9 } then verify A Ōł¬
(B Ōł®C ) = (A Ōł¬ B ) Ōł®
(A Ōł¬C) .
Solution
Given A = {
0,2,4,6,8 } , B = { 2,3,5,7 } and C = { 5,6,7,8 }
First, we find B Ōł®C = {5,7 }, A Ōł¬(B Ōł®C) = {0,2,4,5, 6,7,8} ... (1)
Next, A Ōł¬ B = { 0,2,3,4,5,6,7,8
} , AŌł¬C= { 0,2,4,5,6,7,8 }
Then, (A Ōł¬ B) Ōł® (A Ōł¬C) = { 0,2,4,5,6,7,8 } ... (2)
From
(1) and (2), it is verified that A Ōł¬ (B Ōł®C ) = (A Ōł¬ B ) Ōł®
(A Ōł¬C).
Example 1.22
Verify
A Ōł® (B Ōł¬C ) = (A Ōł®
B ) Ōł¬ (A
Ōł®C) using Venn diagrams.
Solution
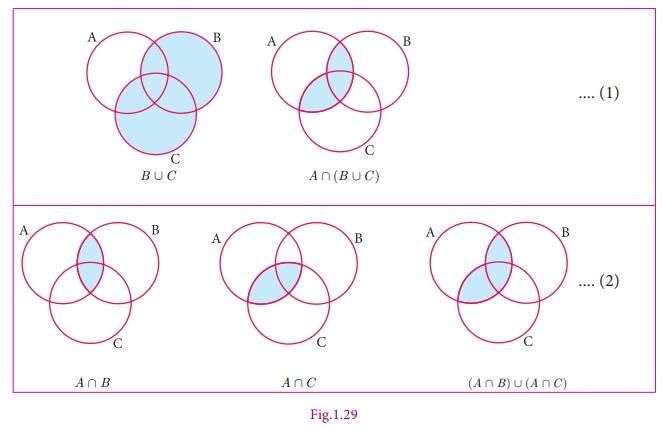
From
(1) and (2), A Ōł®
(B Ōł¬C ) = (A Ōł® B ) Ōł¬ (A Ōł®C) is verified.
Related Topics