Set Language: Introduction

SET LANGUAGE

Introduction

In our daily life, we often deal with collection of objects like books, stamps, coins, etc. Set language is a mathematical way of representing a collection of objects.

Study the problem: 16 students play only Cricket, 18 students play only Volley ball and 3 students play both Cricket and Volley ball, while 2 students play neither Cricket nor Volley ball. Totally 39 students are there in a class.

We can describe this pictorially as follows:

What do the circles in the picture represent? They are collections of students who play games. We do not need to draw 39 students, or even 39 symbols, or use different colours to distinguish those who play Cricket from those who play Volleyball etc. Simply calling the collections C and V is enough; we can talk of those in both C and V, in neither and in one but not the other.  This is the language of sets. A great deal of mathematics is written in this language and hence we are going to study it.

But why is this language so important, why should mathematicians want to use this language? One reason is that everyday language is imprecise and can cause confusion. For example, if I write 1, 2, 3,… what do the three dots at the end mean? You say,“Of course, they mean the list of natural numbers”. What if I write 1, 2, 4,…? What comes next ? It could be 7, and then 11, and so on. (Can you see why ?) Or it could be continued as 8, 16, and so on. If we explicitly say, “The collection of numbers that are powers of 2”, then we know that the latter is meant. So, in general, when we are talking of collections of numbers, we may refer to some collection in some short form, but writing out the collection may be difficult. It is here that the language of sets is of help. We can speak of the powers of 2 as a set of numbers.

Note, this is a list that goes on forever, so it is an infinite set. By now, we have come across several infinite sets: the set of natural numbers, the set of integers, the set of rational numbers, and many more. We also know the set of prime numbers, again an infinite set. But we know many finite sets too. The number of points of intersection of three lines on the plane is an example.

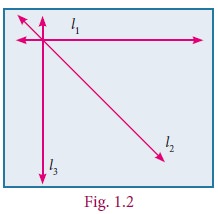
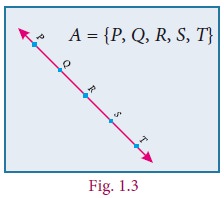
We talk of a point being on a line and we know that a line contains inifinite number of points. For example, five points P,Q,R,S and T which lie on a line can be denoted by a set A= {P, Q, R, S, T}.

We can already see that many of these sets are important in whatever algebra and geometry we have learnt, and we expect that there will be more important sets coming along as we learn mathematics. That is why we are going to learn the language of sets. For now, we will work with small finite sets and learn its language.

Let us look at the following pictures. What do they represent?

Here, Fig.1.4 represents a collection of fruits and Fig. 1.5 represents a collection of house- hold items.

We observe in the above cases, our attention turns from one individual object to a collection of objects based on their characteristics. Any such collection is called a set.