Solved Example Problems | Mathematics - Set Operations | 9th EM Mathematics : Set Language
Chapter: 9th EM Mathematics : Set Language
Set Operations
Set Operations
We started with numbers and very soon we learned
arithmetical operations on them. In algebra we learnt expressions and soon
started adding and multiplying them as well, writing (x2+2) (x-3)
etc. Now that we know sets, the natural question is, what can we do with sets,
what are natural operations on them ?
What can we do with sets ? We can pick an element.
But then which element ? There are many in general, and hence “picking an
element” is not an operation on a set. But like we did with addition,
subtraction etc, we can try and think of operations that combine two given sets
to get a new set. How can we do this ?
A simple way is to put the two sets together. This
gives us a new set, and exactly one set, so it is an operation. We could pick
out exactly the common elements of the two given sets. That’s an interesting
operation too. We could talk of all the elements not in the given set. But this
is problematic: we can list the elements in a set, but which are the elements
not in it ? Almost anything. We know that 5734 is in the set of natural
numbers, but we also know that my chair is not in it, an elephant is not in it,
and so on. How could we ever hope to describe all these elements ? But then
when we speak of sets of numbers we are clearly not talking of elephants ! So
we should really speak of numbers not in the set of natural numbers. For
instance we could implicitly fix the integers and talk of integers not in the
set of natural numbers. In general, we call this “fixed” set the universal set
(relative to which we speak of what is or not in a given set).
When two or more sets combine together to form one
set under the given conditions, then operations on sets can be carried out. We
can visualize the relationship between sets and set operations using Venn
diagram.
1. Universal Set
A Universal set is a set which contains all the
elements of all the sets under consideration and is usually denoted by U.
For example,
i. If we discuss about elements in Natural numbers,
then the universal set U is the set of all Natural numbers. U={x : x
∈ N}.
ii. If A={earth,
mars, jupiter}, then the universal set U is the planets of solar system.
2. Complement of a Set
The Complement of a set A is the set of all elements of U (the universal set) that are not
in A.
It is denoted by A′ or Ac. In symbols A′= {x : x∈U, x∉A}
Venn diagram for complement of a set
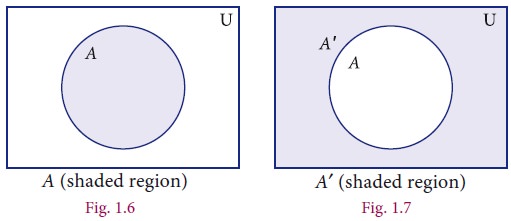
For example,
If U = {all boys in a class} and A= {boys who play Cricket}, then
complement of the set A is A′= {boys
who do not play Cricket}.
Example 1.9
If U = {c, d, e, f,
g, h, i, j} and A = { c, d, g,
j} , find A′.
Solution
U = {c, d, e,
f, g, h, i, j},
A = {c, d, g, j}
A′ ={e,
f, h, i}

3. Union of Two Sets
The union of two sets A and B is the set of all elements which are either in A or in B or in both. It is denoted by A∪B and read
as A union B.
In symbol, A∪B = {x : x
∈A or x∈B}
The union of two sets can be represented by Venn diagram as given below
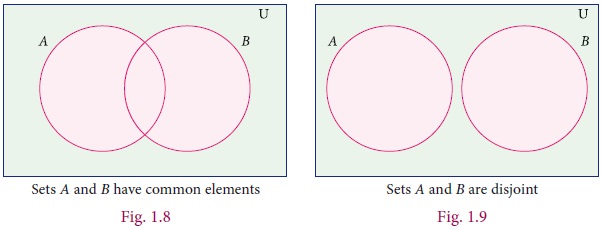
For example,
If P
={Asia,Africa, Antarctica, Australia} and Q
= {Europe, North America, South America}, then the union set of P and Q is P∪Q = {Asia,
Africa, Antartica, Australia, Europe, North America, South America}.

Example 1.10
If A={1, 2, 6} and B={2, 3,
4} , find A∪B.
Solution
Given A={1,
2, 6}, B={2, 3, 4}
A∪B={1, 2,
3, 4,6}.
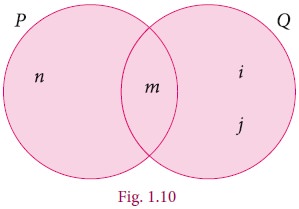
Example 1.11
If P={m, n} and Q= {m, i, j},
represent P and Q in Venn diagram and find P∪Q.
Solution
Given P={m, n}
and Q= {m, i, j}
From the diagram,
P∪Q={n,
m, i, j}.
4. Intersection of TwoSets
The intersection of two sets A and B is the set of all
elements common to both A and B. It is denoted by A∩B and read as A intersection B.
In symbol , A∩B={x : x∈A and x∈B}
Intersection of two sets can be represented by a Venn diagram as given below
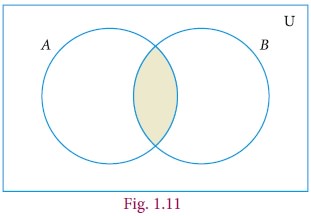
For example,
If A =
{1, 2, 6}; B = {2, 3, 4}, then A∩B = {2}
because 2 is common element of the sets A
and B.

Can we determine n(A ∩ B) in terms of n(A) and n(B)? This seems to be
difficult, but what about n(A ∪ B) in terms of n(A) and n(B)
?
Notice that all the elements in A are in (A ∪ B), and all the elements in B also in A ∪ B
Can we say that n(A ∪ B) = n(A) + n(B) ?
Unfortunately not. Consider an element is common to
both A and B? Of course it is in A union B, but is counted both in A and in B and we don’t want to count the same element twice in A union B !
So indeed, n(A ∪ B) = n(A) + n(B) – n(A ∩ B). But then it is easy to see that n(A
∩B) = n(A)
+ n(B) – n(A ∪ B). So
between the union and the intersection we need to know one to determine the other, given n(A) and n(B).
Example 1.12
Let
A = {x : x is an even natural
number and 1< x ≤ 12} and
B = { x : x is a multiple of
3, x ∈ N
and x≤12} be two sets. Find A∩B.
Solution
Here A = {2, 4, 6, 8, 10, 12} and B = {3, 6, 9, 12}
A∩B = {6, 12}
Example 1.13
If A = {2, 3} and C = { },
find A∩C.
Solution
There is no common element and hence A∩C ={ }

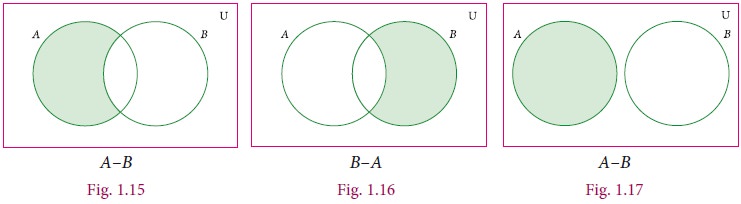
5. Difference of Two Sets
Let A and
B be two sets, the difference of sets
A and B is the set of all elements which are in A, but not in B. It is
denoted by A–B or A\B and read as A difference B.
In symbol, A–B = { x : x ∈ A and x ∉ B}
B–A = { y :
y ∈ B and y ∉ A}.
Venn diagram for set difference
Example 1.14
If A={–3, –2, 1, 4} and B=
{0, 1, 2, 4}, find (i) A–B (ii) B–A.
Solution
A–B ={–3, -2, 1, 4} – {0, 1, 2, 4} = { -3,
-2}
B–A = {0, 1, 2, 4} –{–3, -2, 1, 4} = { 0,
2}

6. Symmetric Difference of Sets
The symmetric difference of two sets A and B is the set (A–B)∪(B–A). It is denoted by AΔB.
A B={ x : x ∈ A–B or
x ∈ B–A}
Example 1.15
If A = {6, 7, 8, 9} and B={8,
10, 12}, find AΔB.
Solution
A–B = {6, 7, 9}
B–A = {10, 12}
AΔB = (A–B)∪(B–A) = {6, 7, 9}∪{10,12}
AΔB = {6, 7, 9, 10, 12}.
Example 1.16
Represent AΔB through Venn diagram.
Solution
AΔB= (A–B) ∪ (B–A)


7. Disjoint Sets
Two sets A
and B are said to be disjoint if they
do not have common elements.
In other words, if A∩B=∅, then A and B are said to be
disjoint sets.
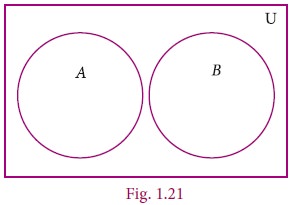
Example 1.17
Verify whether A={20, 22, 23, 24} and B={25,
30, 40, 45} are disjoint sets.
Solution
A = {20,22, 23, 24} , B={25, 30, 40, 45}
A∩B = {20,22,
23, 24} ∩ {25, 30,
40, 45}
= { }
Since A∩B = ∅, A and B are disjoint sets.

Example 1.18
From the given Venn diagram, write
the elements of
(i) A (ii) B (iii) A–B
(iv) B–A (v) A′ (vi) B′ (vii) U
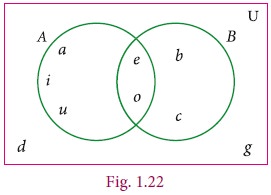
Solution
(i) A =
{a, e, i, o, u}
(ii) B =
{b, c, e, o}
(iii) A–B
= {a, i, u}
(iv) B–A
= {b, c}
(v) A′ =
{b, c, d, g}
(vi) B′ =
{a, d, g, i, u}
(vii) U =
{a, b, c, d, e, g, i, o, u}
Example 1.19
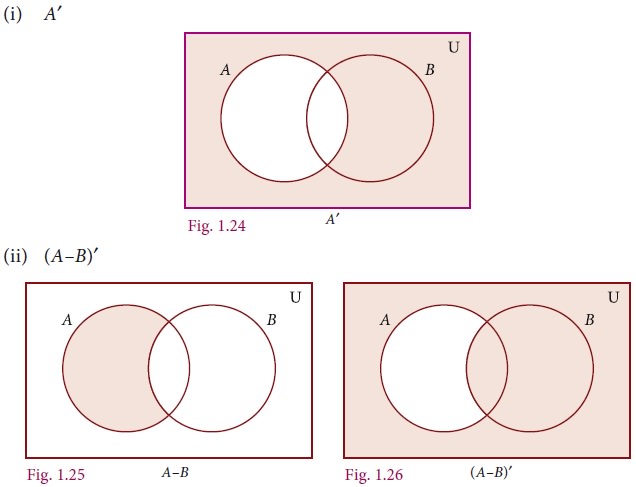
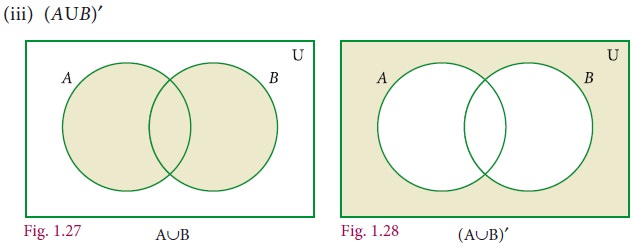
Draw a Venn diagram similar to one at
the side and shade the region representing the following sets
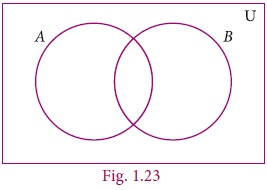
(i) A′ (ii) (A–B)′
(iii) (A∪B)′
Solution
Related Topics