Selecting an Analytical Method

Selecting an Analytical Method

A method is the application of a technique to a specific analyte in a specific matrix. Methods for determining the concentration of lead in drinking water can be devel- oped using any of the techniques mentioned in the previous section. Insoluble lead salts such as PbSO₄ and PbCrO₄ can form the basis for a gravimetric method. Lead forms several soluble complexes that can be used in a complexation titrimetric method or, if the complexes are highly absorbing, in a spectrophotometric method. Lead in the gaseous free-atom state can be measured by an atomic ab- sorption spectroscopic method. Finally, the availability of multiple oxidation states (Pb, Pb2+, Pb4+) makes coulometric, potentiometric, and voltammetric methods feasible.

The requirements of the analysis determine the best method. In choosing a method, consideration is given to some or all the following design criteria: accuracy, precision, sensitivity, selectivity, robustness, ruggedness, scale of operation, analysis time, availability of equipment, and cost. Each of these criteria is considered in more detail in the following sections.

Accuracy

Accuracy is a measure of how closely the result of an experiment agrees with the ex- pected result. The difference between the obtained result and the expected result is usually divided by the expected result and reported as a percent relative error

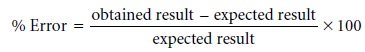
Analytical methods may be divided into three groups based on the magnitude of their relative errors.3 When an experimental result is within 1% of the correct result, the analytical method is highly ac- curate. Methods resulting in relative errors between 1% and 5% are moderately accurate, but methods of low accuracy produce rel- ative errors greater than 5%.

The magnitude of a method’s relative error depends on how accurately the signal is measured, how accurately the value of k in equations 3.1 or 3.2 is known, and the ease of handling the sample without loss or contamination. In general, total analysis methods produce results of high accuracy, and concentration methods range from high to low accuracy.

Precision

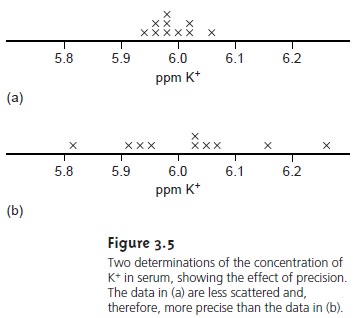
When a sample is analyzed several times, the individual results are rarely the same. Instead, the results are randomly scattered. Precision is a measure of this variability. The closer the agreement between individual analyses, the more precise the results. For example, in determining the concentration of K+ in serum, the results shown in Figure 3.5(a) are more precise than those in Figure 3.5(b). It is important to realize that precision does not imply accuracy. That the data in Figure 3.5(a) are more pre- cise does not mean that the first set of results is more accurate. In fact, both sets of results may be very inaccurate.

As with accuracy, precision depends on those factors affecting the relationship between the signal and the analyte (equations 3.1 and 3.2). Of particular impor- tance are the uncertainty in measuring the signal and the ease of handling samples reproducibly. In most cases the signal for a total analysis method can be measured with a higher precision than the corresponding signal for a concentration method.

Sensitivity

The ability to demonstrate that two samples have different amounts of analyte is an essential part of many analyses. A method’s sensitivity is a measure of its ability to establish that such differences are significant. Sensitivity is often confused with a method’s detection limit.4 The detection limit is the smallest amount of analyte that can be determined with confidence. The detection limit, therefore, is a statisti- cal parameter.

Sensitivity is the change in signal per unit change in the amount of analyte and is equivalent to the proportionality constant, k, in equations 3.1 and 3.2. If ∆S_A is the smallest increment in signal that can be measured, then the smallest difference in the amount of analyte that can be detected is

Suppose that for a particular total analysis method the signal is a measurement of mass using a balance whose smallest increment is ±0.0001 g. If the method’s  sensitivity is 0.200, then the method can conceivably detect a difference of as little as

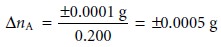
in the absolute amount of analyte in two samples. For methods with the same ∆S_A, the method with the greatest sensitivity is best able to discriminate among smaller amounts of analyte.

Selectivity

An analytical method is selective if its signal is a function of only the amount of an- alyte present in the sample. In the presence of an interferent, equations 3.1 and 3.2 can be expanded to include a term corresponding to the interferent’s contribution to the signal, S_I,

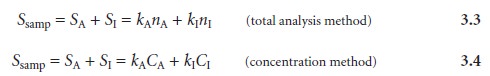
where S_samp is the total signal due to constituents in the sample; k_A and k_I are the sensitivities for the analyte and the interferent, respectively; and n_I and C_I are the moles (or grams) and concentration of the interferent in the sample.

The selectivity of the method for the interferent relative to the analyte is de- fined by a selectivity coefficient, K_A,I

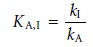                  3.5

which may be positive or negative depending on whether the interferent’s effect on

the signal is opposite that of the analyte.* A selectivity coefficient greater than +1 or less than –1 indicates that the method is more selective for the interferent than for the analyte. Solving equation 3.5 for k_I

k_I = K_A,I x k_A            …………..3.6                                            

substituting into equations 3.3 and 3.4, and simplifying gives

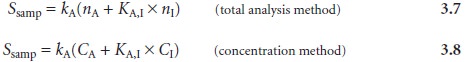
The selectivity coefficient is easy to calculate if k_A and k_I can be independently determined. It is also possible to calculate K_A,I by measuring S_samp in the presence and absence of known amounts of analyte and interferent.

Knowing the selectivity coefficient provides a useful way to evaluate an inter- ferent’s potential effect on an analysis. An interferent will not pose a problem as long as the term K_A,I x n_I in equation 3.7 is significantly smaller than n_A, or K_A,I x C_I in equation 3.8 is significantly smaller than C_A.

Not surprisingly, methods whose signals depend on chemical reactivity are often less selective and, therefore, more susceptible to interferences. Problems with selec- tivity become even greater when the analyte is present at a very low concentration.

Robustness and Ruggedness

For a method to be useful it must provide reliable results. Unfortunately, methods are subject to a variety of chemical and physical interferences that contribute uncer- tainty to the analysis. When a method is relatively free from chemical interferences, it can be applied to the determination of analytes in a wide variety of sample matri- ces. Such methods are considered robust.

Random variations in experimental conditions also introduce uncertainty. If a method’s sensitivity is highly dependent on experimental conditions, such as tem- perature, acidity, or reaction time, then slight changes in those conditions may lead to significantly different results. A rugged method is relatively insensitive to changes in experimental conditions.

Scale of Operation

Another way to narrow the choice of methods is to consider the scale on which the analysis must be conducted. Three limitations of particular importance are the amount of sample available for the analysis, the concentration of analyte in the sample, and the absolute amount of analyte needed to obtain a measurable signal. The first and second limitations define the scale of operations shown in Figure 3.6; the last limitation positions a method within the scale of operations.

The scale of operations in Figure 3.6 shows the analyte’s concentration in weight percent on the y-axis and the sample’s size on the x-axis. For convenience, we divide analytes into major (>1% w/w), minor (0.01% w/w – 1% w/w), trace (10–7% w/w – 0.01% w/w) and ultratrace (<10–7% w/w) components, and we divide samples into macro (>0.1 g), meso (10 mg – 100 mg), micro (0.1 mg – 10 mg) and ultramicro (<0.1 mg) sample sizes. Note that both the x-axis and the y-axis use a logarithmic scale. The analyte’s concentration and the amount of sample used provide a characteristic description for an analysis. For example, samples in a macro–major analysis weigh more than 0.1 g and contain more than 1% analyte.

Diagonal lines connecting the two axes show combinations of sample size and concentration of analyte containing the same absolute amount of analyte. As shown in Figure 3.6, for example, a 1-g sample containing 1% analyte has the same amount of analyte (0.010 g) as a 100-mg sample containing 10% analyte or a 10-mg sample containing 100% analyte.

Since total analysis methods respond to the absolute amount of analyte in a sample, the diagonal lines provide an easy way to define their limitations. Consider, for example, a hypothetical total analysis method for which the minimum de- tectable signal requires 100 mg of analyte. Using Figure 3.6, the diagonal line repre- senting 100 mg suggests that this method is best suited for macro samples and major analytes. Applying the method to a minor analyte with a concentration of 0.1% w/w requires a sample of at least 100 g. Working with a sample of this size is rarely practical, however, due to the complications of carrying such a large amount of material through the analysis. Alternatively, the minimum amount of required analyte can be decreased by improving the limitations associated with measuring the signal. For example, if the signal is a measurement of mass, a decrease in the minimum amount of analyte can be accomplished by switching from a con- ventional analytical balance, which weighs samples to ±0.1 mg, to a semimicro (±0.01 mg) or microbalance (±0.001 mg).

Concentration methods frequently have both lower and upper limits for the amount of analyte that can be determined. The lower limit is dictated by the small- est concentration of analyte producing a useful signal and typically is in the parts per million or parts per billion concentration range. Upper concentration limits exist when the sensitivity of the analysis decreases at higher concentrations.

An upper concentration level is important because it determines how a sam- ple with a high concentration of analyte must be treated before the analysis. Con- sider, for example, a method with an upper concentration limit of 1 ppm (micro- grams per milliliter). If the method requires a sample of 1 mL, then the upper limit on the amount of analyte that can be handled is 1 μg. Using Figure 3.6, and following the diagonal line for 1 μg of analyte, we find that the analysis of an ana- lyte present at a concentration of 10% w/w requires a sample of only 10 μg! Ex- tending such an analysis to a major analyte, therefore, requires the ability to ob- tain and work with very small samples or the ability to dilute the original sample accurately. Using this example, analyzing a sample for an analyte whose concen- tration is 10% w/w requires a 10,000-fold dilution. Not surprisingly, concentra- tion methods are most commonly used for minor, trace, and ultratrace analytes, in macro and meso samples.

Equipment, Time, and Cost

Finally, analytical methods can be compared in terms of their need for equipment, the time required to complete an analysis, and the cost per sample. Methods relying on instrumentation are equipment-intensive and may require significant operator training. For example, the graphite furnace atomic absorption spectroscopic method for determining lead levels in water requires a significant capital investment in the instrument and an experienced operator to obtain reliable results. Other methods, such as titrimetry, require only simple equipment and reagents and can be learned quickly.

The time needed to complete an analysis for a single sample is often fairly simi- lar from method to method. This is somewhat misleading, however, because much of this time is spent preparing the solutions and equipment needed for the analysis. Once the solutions and equipment are in place, the number of samples that can be analyzed per hour differs substantially from method to method. This is a significant factor in selecting a method for laboratories that handle a high volume of samples.

The cost of an analysis is determined by many factors, including the cost of necessary equipment and reagents, the cost of hiring analysts, and the number of samples that can be processed per hour. In general, methods relying on instruments cost more per sample than other methods.

Making the Final Choice

Unfortunately, the design criteria discussed earlier are not mutually independent.8 Working with smaller amounts of analyte or sample, or improving selectivity, often comes at the expense of precision. Attempts to minimize cost and analysis time may decrease accuracy. Selecting a specific method requires a careful balance among these design criteria. Usually, the most important design criterion is accuracy, and the best method is that capable of producing the most accurate results. When the need for results is urgent, as is often the case in clinical labs, analysis time may be- come the critical factor.

The best method is often dictated by the sample’s properties. Analyzing a sam- ple with a complex matrix may require a method with excellent selectivity to avoid interferences. Samples in which the analyte is present at a trace or ultratrace con- centration usually must be analyzed by a concentration method. If the quantity of sample is limited, then the method must not require large amounts of sample.

Determining the concentration of lead in drinking water requires a method that can detect lead at the parts per billion concentrations. Selectivity is also im- portant because other metal ions are present at significantly higher concentrations. Graphite furnace atomic absorption spectroscopy is a commonly used method for determining lead levels in drinking water because it meets these specifications. The same method is also used in determining lead levels in blood, where its ability to detect low concentrations of lead using a few microliters of sample are important considerations.