Language of Analytical Chemistry: Developing the Procedure

Developing the Procedure

After selecting a method, it is necessary to develop a procedure that will accomplish the goals of the analysis. In developing the procedure, attention is given to compen- sating for interferences, selecting and calibrating equipment, standardizing the method, acquiring a representative sample, and validating the method.

Compensating for Interferences

The accuracy of a method depends on its selectivity for the analyte. Even the best methods, however, may not be free from interferents that contribute to the mea- sured signal. Potential interferents may be present in the sample itself or the reagents used during the analysis. In this section we will briefly look at how to mini- mize these two sources of interference.

In the absence of an interferent, the total signal measured during an analysis, S_meas, is a sum of the signal due to the analyte, and the signal due to the rea- gents, S_reag

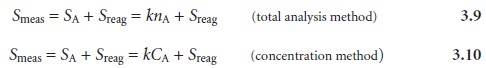
Without an independent determination of S_reag, equation 3.9 or 3.10 cannot be solved for the moles or concentration of analyte. The contribution of S_reag is deter- mined by measuring the signal for a reagent or method blank that does not contain the sample. Consider, for example, a procedure in which a 0.1-g sample is dissolved in 100 mL of solvent. After dissolving the sample, several reagents are added, and the signal is measured. The reagent blank is prepared by omitting the sample and adding the reagents to 100 mL of solvent. When the sample is a liquid, or is in solu- tion, an equivalent volume of an inert solvent is substituted for the sample. Once S_reag is known, it is easy to correct S_meas for the reagent’s contribution to the overall signal.

Compensating for an interference in the sample’s matrix is more difficult. If the identity and concentration of the interferent are known, then it can be added to the reagent blank. In most analyses, however, the identity or concentration of matrix interferents is not known, and their contribution to S_meas is not included in S_reag. In- stead, the signal from the interferent is included as an additional term

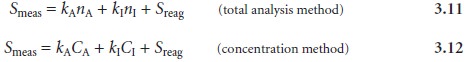
Solving either equation 3.11 or 3.12 for the amount of analyte can be accomplished by separating the analyte and interferent before the analysis, thus eliminating the term for the interferent.

Alternatively, equations 3.11 or 3.12 can be solved for the amounts of both the analyte and the interferent. To do so, however, we must obtain two independent values for S_meas. Using a concentration method as an example, gives two equations

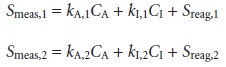
that can be solved simultaneously for C_A and C_I. This treatment is general. The composition of a solution with a total of n analytes and interferents can be deter- mined by measuring n independent signals, and solving n independent simultane- ous equations of the general form of equation 3.11 or 3.12.

Calibration and Standardization

Analytical chemists make a distinction between calibration and standardization.9 Calibration ensures that the equipment or instrument used to measure the signal is operating correctly by using a standard known to produce an exact signal. Balances, for example, are calibrated using a standard weight whose mass can be traced to the internationally accepted platinum–iridium prototype kilogram.

Standardization is the process of experimentally determining the relation- ship between the signal and the amount of analyte (the value of k in equations 3.1 and 3.2). For a total analysis method, standardization is usually defined by the stoichiometry of the chemical reactions responsible for the signal. For a con- centration method, however, the relationship between the signal and the ana- lyte’s concentration is a theoretical function that cannot be calculated without experimental measurements. To standardize a method, the value of k is deter- mined by measuring the signal for one or more standards, each containing a known concentration of analyte. When several standards with different concen- trations of analyte are used, the result is best viewed visually by plotting S_meas versus the concentration of analyte in the standards. Such a plot is known as a calibration curve.

Sampling

Selecting an appropriate method helps ensure that an analysis is accurate. It does not guarantee, however, that the result of the analysis will be sufficient to solve the problem under investigation or that a proposed answer will be correct. These latter concerns are addressed by carefully collecting the samples to be analyzed.

A proper sampling strategy ensures that samples are representative of the mate- rial from which they are taken. Biased or nonrepresentative sampling and contami- nation of samples during or after their collection are two sources of sampling error that can lead to significant errors. It is important to realize that sampling errors are completely independent of analysis errors. As a result, sampling errors cannot be corrected by evaluating a reagent blank.

Validation

Before a procedure can provide useful analytical information, it is necessary to demonstrate that it is capable of providing acceptable results. Validation is an eval- uation of whether the precision and accuracy obtained by following the procedure are appropriate for the problem. In addition, validation ensures that the written procedure has sufficient detail so that different analysts or laboratories following the same procedure obtain comparable results. Ideally, validation uses a standard sam- ple whose composition closely matches the samples for which the procedure was developed. The comparison of replicate analyses can be used to evaluate the proce- dure’s precision and accuracy. Intralaboratory and interlaboratory differences in the procedure also can be evaluated. In the absence of appropriate standards, accuracy can be evaluated by comparing results obtained with a new method to those ob- tained using a method of known accuracy.