Replacement And Maintenance Analysis

REPLACEMENT AND MAINTENANCE ANALYSIS

Introduction

Organizations providing goods/services use several facilities like equipment and machinery which are directly required in their operations. In addition to these facilities, there are several other items which are necessary to facilitate the functioning of organizations.

All such facilities should be continuously monitored for their efficient functioning; otherwise, the quality of service will be poor. Besides the quality of service of the facilities, the cost of their operation and maintenance would increase with the passage of time.

Hence, it is an absolute necessity to maintain the equipment in good operating conditions with economical cost. Thus, we need an integrated approach to minimize the cost of maintenance. In certain cases, the equipment will be obsolete over a period of time.

If a firm wants to be in the same business competitively, it has to take decision on whether to replace the old equipment or to retain it by taking the cost of maintenance and operation into account.

There are two basic reasons for considering the replacement of an equipment physical impairment of the various parts or obsolescence of the equipment.

Physical impairment refers only to changes in the physical condition of the machine itself. This would lead to a decline in the value of the service rendered, increased operating cost, increased maintenance cost or a combination of these.

Obsolescence is due to improvement of the tools of production, mainly improvement in technology.

So, it would be uneconomical to continue production with the same machine under any of the above situations. Hence, the machines are to be periodically replaced.

Sometimes, the capacity of existing facilities may be inadequate to meet the current demand. Under such situation, the following alternatives will be considered.

ü Replacement of the existing equipment with a new one.

ü Augmenting the existing one with an additional equipment.

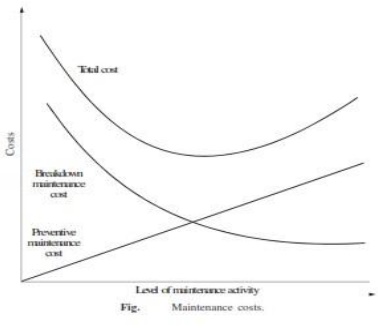
Types of Maintenance

Maintenance activity can be classified into two types:

ü Preventive maintenance and

ü Breakdown maintenance.

Preventive maintenance (PM) is the periodical inspection and service activities which are aimed to detect potential failures and perform minor adjustments or repairs which will prevent major operating problems in future.

Breakdown maintenance is the repair which is generally done after the equipment has attained down state. It is often of an emergency nature which will have associated penalty in terms of expediting cost of maintenance and down time cost of equipment.

Preventive maintenance will reduce such cost up to a point. Beyond that point, the cost of preventive maintenance will be more when compared to the breakdown maintenance cost.

The total cost, which is the sum of the preventive maintenance cost and the breakdown maintenance cost, will go on decreasing with an increase in the level of maintenance up to a point.

Beyond that point, the total cost will start increasing. The level of maintenance corresponding to the minimum total cost is the optimal level of maintenance. The concepts are demonstrated in Fig

Types of Replacement Problem

Replacement study can be classified into two categories:

(a) Replacement of assets that deteriorate with time (Replacement due to gradual failure, or wear and tear of the components of the machines).

This can be further classified into the following types:

(i)      Determination of economic life of an asset.

(ii)   Replacement of an existing asset with a new asset.

(b) Simple probabilistic model for assets which fail completely (replacement due to sudden failure).

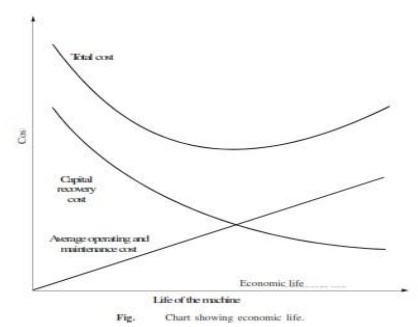
Determination of Economic Life of an Asset

Any asset will have the following cost components:

ü Capital recovery cost (average first cost), computed from the first cost (purchase price) of the machine.

ü Average operating and maintenance cost (O & M cost)

Total cost which is the sum of capital recovery cost (average first cost) and average maintenance cost.

EXAMPLE

A firm is considering replacement of an equipment, whose first cost is Rs. 4,000 and the scrap value is negligible at the end of any year. Based on experience, it was found that the maintenance cost is zero during the first year and it increases by Rs. 200 every year thereafter.

(a)   When should the equipment be replaced if i = 0%?

(b)   When should the equipment be replaced if i = 12%?

(a)   When i = 0%. In this problem

(i)           First cost = Rs. 4,000

(ii)        Maintenance cost is Rs. 0 during the first year and it increases by Rs. 200 every year thereafter.

This is summarized in column B of Table

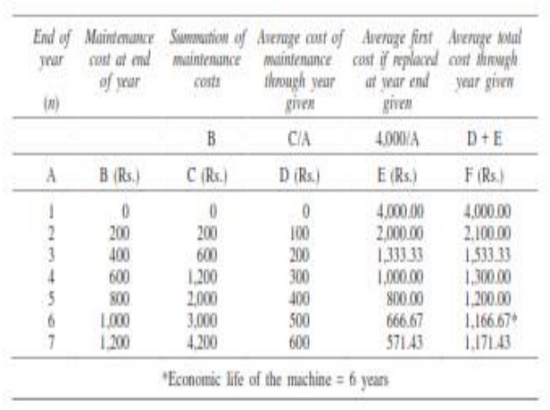
Column C summarizes the summation of maintenance costs for each replacement period. The value corresponding to any end of year in this column represents the total maintenance cost of using the equipment till the end of that particular year.

Average total cost = [ First cost (FC) + Summation of maintenance cost ] / Replacement period

Column F = Column E + Column D

The value corresponding to any end of year (n) in Column F represents the average total cost of using the equipment till the end of that particular year.

For this problem, the average total cost decreases till the end of year 6 and then it increases. Therefore, the optimal replacement period is six years, i.e. economic life of the equipment is six years.

(b) When interest rate, i = 12%. When the interest rate is more than 0%, the steps to be taken for getting the economic life are summarized with reference to Table

Table Calculations to Determine Economic Life (First cost = Rs. 4,000, Interest = 12%)

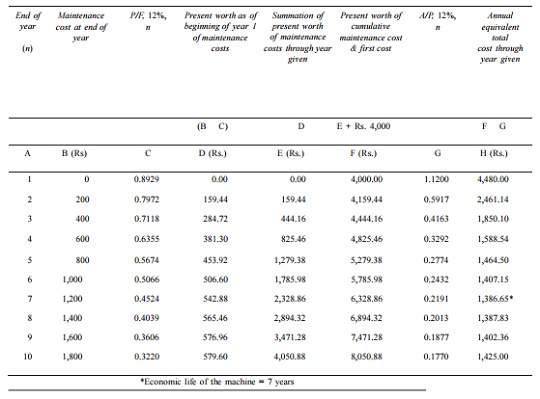
The steps are summarized now:

1. Discount the maintenance costs to the beginning of year 1.

Column D = Column B

1/ (1 + i)ⁿ

= Column B    (P/F, i, n) = Column B    Column C.

2. Find the summation of present worth of maintenance costs through the year given (Column E = Column D).

3. Find Column F by adding the first cost of Rs. 4,000 to Column E.

4. Find the annual equivalent total cost through the years given.

Column H = Column F       i(1 + i)ⁿ                 / (1 + i)ⁿ      − 1   

= Column F     (A/P, 12%, n) = Column F    Column G    

5. Identify the end of year for which the annual equivalent total cost is minimum.

For this problem, the annual equivalent total cost is minimum at the end of year 7. Therefore, the economic life of the equipment is seven years.

Replacement Of Exist Ing Asset With A New Asset

In this section, the c oncept of comparison of replacement of an existing asset with a new asset is presented. In this analysis, the annual equivalent cost of each alternative should be co mputed first.

Then the alternative which has the least cost should be selected as the best alternative. Before discu ssing details, some preliminary concepts whic h are essential for this type of replacem ent analysis are presented.

Capital Recovery with Return

Consider the follow ing data of a machine.

Let

P = purchase priice of the machine,

F = salvage valu e of the machine at the end of machine life,

n = life of the m achine in years, and

i = interest rate,, compounded annually

The corresponding cash flow diagram is shown in Fig

The equation for the annual equivalent amount for the above cash flow diagram is

AE(i) = (P – F )    (A/P, i, n) + F    i

This equation represents the capital recovery with return.

Concept of Challenger and Defender

o   If an existing equipment is considered for replacement with a new equipment, then the existing equipment is known as the defender and the new equipment is known as challenger.

o   Assume that an equipment has been purchased about three years back for Rs. 5,00,000 and it is considered for replacement with a new equipment. The supplier of the new equipment will take the old one for some money, say, Rs. 3,00,000.

o   This should be treated as the present value of the existing equipment and it should be considered for all further economic analysis.

o   The purchase value of the existing equipment before three years is now known as sunk cost, and it should not be considered for further analysis.

EXAMPLE

Two years ago, a machine was purchased at a cost of Rs. 2,00,000 to be useful for eight years. Its salvage value at the end of its life is Rs. 25,000. The annual maintenance cost is Rs. 25,000.

The market value of the present machine is Rs. 1,20,000. Now, a new machine to cater to the need of the present machine is available at Rs. 1,50,000 to be useful for six years. Its annual maintenance cost is Rs. 14,000. The salvage value of the new machine is Rs. 20,000.

Using an interest rate of 12%, find whether it is worth replacing the present machine with the new machine.

Solution

Alternative 1—

Present machine

Purchase price = Rs. 2,00,000

Present value (P) = Rs. 1,20,000

Salvage value (F) = Rs. 25,000

Annual maintenance cost (A) = Rs. 25,000

Remaining life = 6 years

Interest rate = 12%

The cash flow diagram of the present machine is illustrated in Fig.

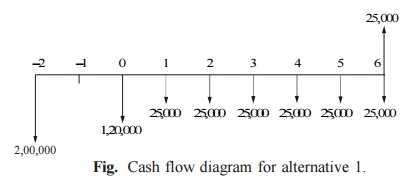
Fig.  Cash flow diagram for alternative 1.

annual maintenance cost for the preceding periods are not shown in this figure. The annual equivalent cost is computed as

AE(12%) = (P – F)(A/P, 12%, 6) + F    i + A

= (1,20,000 – 25,000)(0.2432) + 25,000    0.12 + 25,000

= Rs. 51,104

Alternative 2 —

New machine

Purchase price (P) = Rs. 1,50,000

Salvage value (F) = Rs. 20,000

Annual maintenance cost (A) = Rs. 14,000

Life = 6 years

Interest rate = 12%

The cash flow diagram of the new machine is depicted in Fig.

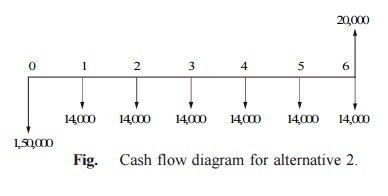
Fig.        Cash flow diagram for alternative 2.

The formula for the annual equivalent cost is

AE(12%) = (P – F)(A/P, 12%, 6) + F    i + A

= (1,50,000 – 20,000)(0.2432) + 20,000    0.12 + 14,000

= Rs. 48,016

Since the annual equivalent cost of the new machine is less than that of the present machine, it is suggested that the present machine be replaced with the new machine.

Simple Probabilistic Model For Items Which Fail Completely

Electronic items like transistors, resistors, tubelights, bulbs, etc. could fail all of a sudden, instead of gradual deterioration. The failure of the item may result in complete breakdown of the system. The system may contain a collection of such items or just one item, say a tubelight.

Therefore, we use some replacement policy for such items which would avoid the possibility of a complete breakdown.

The following are the replacement policies which are applicable for this situation.

(i)  Individual replacement policy. Under this policy, an item is replaced immediately after its failure.

(ii) Group replacement policy.  Under this policy, the following decision is

made:

At what equal intervals are all the items to be replaced simultaneously with a provision to replace the items individually which fail during a fixed group replacement period?

There is a trade-off between the individual replacement policy and the group replacement policy. Hence, for a given problem, each of the replacement policies is evaluated and the most economical policy is selected for implementation. This is explained with two numerical problems.

EXAMPLE

The failure rates of transistors in a computer are summarized in Table .

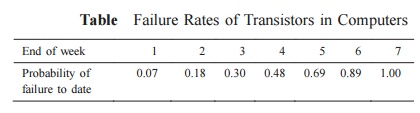
The cost of replacing an individual failed transistor is Rs. 9. If all the transistors are replaced simultaneously, it would cost Rs. 3.00 per transistor. Any one of the following two options can be followed to replace the transistors:

(a)  Replace the transistors individually when they fail (individual replacement policy).

(b) Replace all the transistors simultaneously at fixed intervals and replace the individual transistors as they fail in service during the fixed interval (group replacement policy).

Find out the optimal replacement policy, i.e. individual replacement policy or group replacement policy. If group replacement policy is optimal, then find at what equal intervals should all the transistors be replaced.

Solution

Assume that there are 100 transistors in use.

Let,

p_i be the probability that a transistor which was new when placed in position for use, fails during the ith week of its life. Hence,

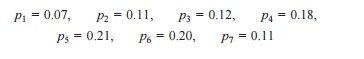
Since the sum of p_is is equal to 1 at the end of the 7th week, the transistors are sure to fail during the seventh week.

Assume that

(a)  transistors that fail during a week are replaced just before the end of the week, and

(b) the actual percentage of failures during a week for a sub-group of transistors with the same age is same as the expected percentage of failures during the week for that sub-group of transistors.

Let

Ni  = the number of transistors replaced at the end of the ith week

N0 = number of transistors replaced at the end of the week 0 (or at the beginning of the first week).

= 100

N1 = number of transistors replaced at the end of the 1st week

= N0  p1 = 100     0.07 = 7                        

N2 = number of transistors replaced at the end of the 2nd week

= N0  p2 + N1                p1                                 

= 100 0.11   + 7    0.07   = 12           

N3 = N0    p3 + N1       p2 + N2      p1              

= 100 0.12   + 7    0.11   + 12  0.07  

= 14                                                                     

N4 = N0    p4 + N1       p3 + N2      p2 + N3    p1      

= 100 0.18   + 7    0.12   + 12  0.11 + 14    0.07

= 21                                                                     

N5 = N0    p5 + N1       p4 + N2      p3 + N3    p2 + N4    p1

= 100 0.21   + 7    0.18   + 12  0.12 + 14    0.11 + 21    0.07

= 27                                                                     

N6 = N0     p6 + N1      p5 + N2      p4 + N3      p3 + N4      p2 + N5      p1

= 100 0.2 + 7        0.21 + 12    0.18 + 14   0.12 + 21     0.11 + 27    0.07

= 30                                                                     

N7 = N0     p7 + N1      p6 + N2      p5 + N3      p4 + N4      p3 + N5      p2

+ N6  p1                                                    

= 100 0.11 + 7      0.2 + 12    0.21 + 14      0.18 + 21    0.12  

+ 27  0.11 + 30    0.07                              

= 25                                                                     

Calculation of individual replacement cost

Expected life of each transistor =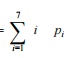  

= 1   0.07 + 2   0.11 + 3   0.12 + 4   0.18

+ 5    0.21 + 6    0.2 + 7    0.11

= 4.39 weeks

Average No. of failures/week = 100/4.39 = 23

(approx.) Therefore,

Cost of individual replacement

= (No. of failures/week Individual replacement cost/transistor) = 23 9 = Rs. 207.

Determination of group replacement cost

Cost of transistor when replaced  simultaneously = Rs. 3

Cost of transistor when replaced individually = Rs. 9

The costs of group replacement policy for several replacement periods are summarized in Table.

Table  Calculations of Cost for Preventive Maintenance

From Table it is clear that the average cost/week is minimum for the fourth week. Hence, the group replacement period is four weeks.

Individual replacement cost/week = Rs. 207

Minimum group replacement cost/week = Rs. 196.50

Since the minimum group replacement cost/week is less than the individual replacement cost/week, the group replacement policy is the best, and hence all the transistors should be replaced once in four weeks and the transistors which fail during this four-week period are to be replaced individually.