Chapter: Mechanical : Engineering Economics & Cost Analysis : Replacement And Maintenance Analysis
Simple Probabilistic Model For Items Which Fail Completely
Simple Probabilistic Model For Items Which Fail Completely
Electronic items like transistors, resistors, tubelights, bulbs, etc. could fail all of a sudden, instead of gradual deterioration. The failure of the item may result in complete breakdown of the system. The system may contain a collection of such items or just one item, say a tubelight.
Therefore, we use some replacement policy for such items which would avoid the possibility of a complete breakdown.
The following are the replacement policies which are applicable for this situation.
(i) Individual replacement policy. Under this policy, an item is replaced immediately after its failure.
(ii) Group replacement policy. Under this policy, the following decision is
made:
At what equal intervals are all the items to be replaced simultaneously with a provision to replace the items individually which fail during a fixed group replacement period?
There is a trade-off between the individual replacement policy and the group replacement policy. Hence, for a given problem, each of the replacement policies is evaluated and the most economical policy is selected for implementation. This is explained with two numerical problems.
EXAMPLE
The failure rates of transistors in a computer are summarized in Table .
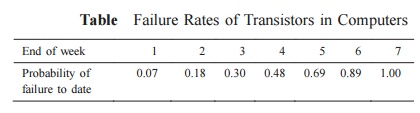
The cost of replacing an individual failed transistor is Rs. 9. If all the transistors are replaced simultaneously, it would cost Rs. 3.00 per transistor. Any one of the following two options can be followed to replace the transistors:
(a) Replace the transistors individually when they fail (individual replacement policy).
(b) Replace all the transistors simultaneously at fixed intervals and replace the individual transistors as they fail in service during the fixed interval (group replacement policy).
Find out the optimal replacement policy, i.e. individual replacement policy or group replacement policy. If group replacement policy is optimal, then find at what equal intervals should all the transistors be replaced.
Solution
Assume that there are 100 transistors in use.
Let,
pi be the probability that a transistor which was new when placed in position for use, fails during the ith week of its life. Hence,
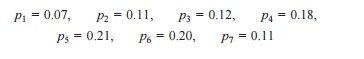
Since the sum of pis is equal to 1 at the end of the 7th week, the transistors are sure to fail during the seventh week.
Assume that
(a) transistors that fail during a week are replaced just before the end of the week, and
(b) the actual percentage of failures during a week for a sub-group of transistors with the same age is same as the expected percentage of failures during the week for that sub-group of transistors.
Let
Ni = the number of transistors replaced at the end of the ith week
N0 = number of transistors replaced at the end of the week 0 (or at the beginning of the first week).
= 100
N1 = number of transistors replaced at the end of the 1st week
= N0 p1 = 100 0.07 = 7
N2 = number of transistors replaced at the end of the 2nd week
= N0 p2 + N1 p1
= 100 0.11 + 7 0.07 = 12
N3 = N0 p3 + N1 p2 + N2 p1
= 100 0.12 + 7 0.11 + 12 0.07
= 14
N4 = N0 p4 + N1 p3 + N2 p2 + N3 p1
= 100 0.18 + 7 0.12 + 12 0.11 + 14 0.07
= 21
N5 = N0 p5 + N1 p4 + N2 p3 + N3 p2 + N4 p1
= 100 0.21 + 7 0.18 + 12 0.12 + 14 0.11 + 21 0.07
= 27
N6 = N0 p6 + N1 p5 + N2 p4 + N3 p3 + N4 p2 + N5 p1
= 100 0.2 + 7 0.21 + 12 0.18 + 14 0.12 + 21 0.11 + 27 0.07
= 30
N7 = N0 p7 + N1 p6 + N2 p5 + N3 p4 + N4 p3 + N5 p2
+ N6 p1
= 100 0.11 + 7 0.2 + 12 0.21 + 14 0.18 + 21 0.12
+ 27 0.11 + 30 0.07
= 25
Calculation of individual replacement cost
Expected life of each transistor = 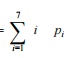
= 1 0.07 + 2 0.11 + 3 0.12 + 4 0.18
+ 5 0.21 + 6 0.2 + 7 0.11
= 4.39 weeks
Average No. of failures/week = 100/4.39 = 23
(approx.) Therefore,
Cost of individual replacement
= (No. of failures/week Individual replacement cost/transistor) = 23 9 = Rs. 207.
Determination of group replacement cost
Cost of transistor when replaced simultaneously = Rs. 3
Cost of transistor when replaced individually = Rs. 9
The costs of group replacement policy for several replacement periods are summarized in Table.
Table Calculations of Cost for Preventive Maintenance

From Table it is clear that the average cost/week is minimum for the fourth week. Hence, the group replacement period is four weeks.
Individual replacement cost/week = Rs. 207
Minimum group replacement cost/week = Rs. 196.50
Since the minimum group replacement cost/week is less than the individual replacement cost/week, the group replacement policy is the best, and hence all the transistors should be replaced once in four weeks and the transistors which fail during this four-week period are to be replaced individually.
Related Topics