Relationship Types of Degree Higher than Two

Relationship Types of Degree Higher than Two

In Section 7.4.2 we defined the degree of a relationship type as the number of participating entity types and called a relationship type of degree two binary and a relationship type of degree three ternary. In this section, we elaborate on the differences between binary and higher-degree relationships, when to choose higher-degree versus binary relationships, and how to specify constraints on higher-degree relation-ships.

1. Choosing between Binary and Ternary (or Higher-Degree) Relationships

The ER diagram notation for a ternary relationship type is shown in Figure 7.17(a), which displays the schema for the SUPPLY relationship type that was displayed at the entity set/relationship set or instance level in Figure 7.10. Recall that the relationship set of SUPPLY is a set of relationship instances (s, j, p), where s is a SUPPLIER who is currently supplying a PART p to a PROJECT j. In general, a relationship type R of degree n will have n edges in an ER diagram, one connecting R to each participating entity type.

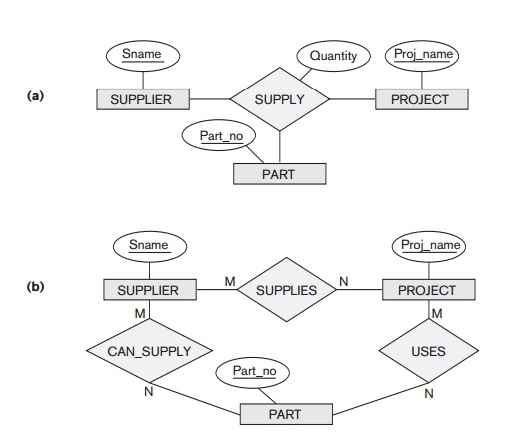
Figure 7.17(b) shows an ER diagram for three binary relationship types CAN_SUPPLY, USES, and SUPPLIES. In general, a ternary relationship type repre-sents different information than do three binary relationship types. Consider the three binary relationship types CAN_SUPPLY, USES, and SUPPLIES. Suppose that CAN_SUPPLY, between SUPPLIER and PART, includes an instance (s, p) whenever supplier s can supply part p (to any project); USES, between PROJECT and PART, includes an instance ( j, p) whenever project j uses part p; and SUPPLIES, between SUPPLIER and PROJECT, includes an instance (s, j) whenever supplier s supplies

some part to project j. The existence of three relationship instances (s, p), ( j, p), and (s, j) in CAN_SUPPLY, USES, and SUPPLIES, respectively, does not necessarily imply that an instance (s, j, p) exists in the ternary relationship SUPPLY, because the meaning is different. It is often tricky to decide whether a particular relationship should be represented as a relationship type of degree n or should be broken down into several relationship types of smaller degrees. The designer must base this decision on the semantics or meaning of the particular situation being represented. The typical solution is to include the ternary relationship plus one or more of the binary relationships, if they represent different meanings and if all are needed by the application.

Some database design tools are based on variations of the ER model that permit only binary relationships. In this case, a ternary relationship such as SUPPLY must be represented as a weak entity type, with no partial key and with three identifying relationships. The three participating entity types SUPPLIER, PART, and PROJECT are together the owner entity types (see Figure 7.17(c)). Hence, an entity in the weak entity type SUPPLY in Figure 7.17(c) is identified by the combination of its three owner entities from SUPPLIER, PART, and PROJECT.

It is also possible to represent the ternary relationship as a regular entity type by introducing an artificial or surrogate key. In this example, a key attribute Supply_id could be used for the supply entity type, converting it into a regular entity type. Three binary N:1 relationships relate SUPPLY to the three participating entity types.

Another example is shown in Figure 7.18. The ternary relationship type OFFERS represents information on instructors offering courses during particular semesters; hence it includes a relationship instance (i, s, c) whenever INSTRUCTOR i offers COURSE c during SEMESTER s. The three binary relationship types shown in Figure 7.18 have the following meanings: CAN_TEACH relates a course to the instructors who can teach that course, TAUGHT_DURING relates a semester to the instructors who taught some course during that semester, and OFFERED_DURING

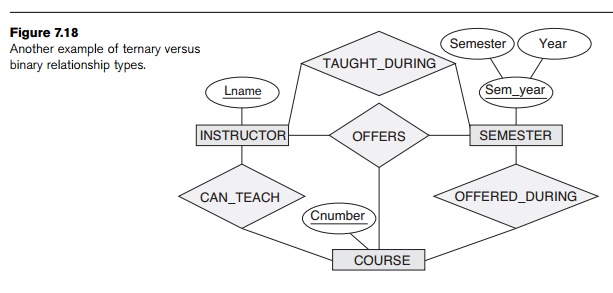
relates a semester to the courses offered during that semester by any instructor. These ternary and binary relationships represent different information, but certain constraints should hold among the relationships. For example, a relationship instance (i, s, c) should not exist in OFFERS unless an instance (i, s) exists in TAUGHT_DURING, an instance (s, c) exists in OFFERED_DURING, and an instance (i, c) exists in CAN_TEACH. However, the reverse is not always true; we may have instances (i, s), (s, c), and (i, c) in the three binary relationship types with no corre-sponding instance (i, s, c) in OFFERS. Note that in this example, based on the mean-ings of the relationships, we can infer the instances of TAUGHT_DURING and OFFERED_DURING from the instances in OFFERS, but we cannot infer the instances of CAN_TEACH; therefore, TAUGHT_DURING and OFFERED_DURING are redundant and can be left out.

Although in general three binary relationships cannot replace a ternary relationship, they may do so under certain additional constraints. In our example, if the CAN_TEACH relationship is 1:1 (an instructor can teach one course, and a course can be taught by only one instructor), then the ternary relationship OFFERS can be left out because it can be inferred from the three binary relationships CAN_TEACH, TAUGHT_DURING, and OFFERED_DURING. The schema designer must analyze the meaning of each specific situation to decide which of the binary and ternary relationship types are needed.

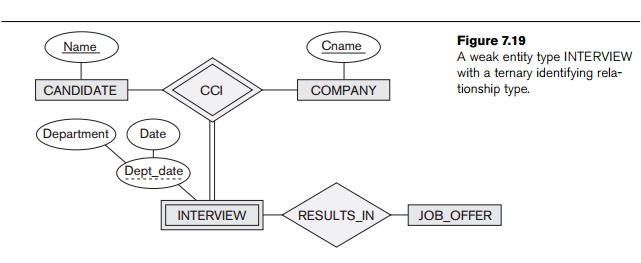
Notice that it is possible to have a weak entity type with a ternary (or n-ary) identi-fying relationship type. In this case, the weak entity type can have several owner entity types. An example is shown in Figure 7.19. This example shows part of a data-base that keeps track of candidates interviewing for jobs at various companies, and may be part of an employment agency database, for example. In the requirements, a candidate can have multiple interviews with the same company (for example, with different company departments or on separate dates), but a job offer is made based on one of the interviews. Here, INTERVIEW is represented as a weak entity with two owners CANDIDATE and COMPANY, and with the partial key Dept_date. An INTERVIEW entity is uniquely identified by a candidate, a company, and the combination of the date and department of the interview.

2. Constraints on Ternary (or Higher-Degree) Relationships

There are two notations for specifying structural constraints on n-ary relationships, and they specify different constraints. They should thus both be used if it is important to fully specify the structural constraints on a ternary or higher-degree relationship. The first notation is based on the cardinality ratio notation of binary relationships displayed in Figure 7.2. Here, a 1, M, or N is specified on each partici-pation arc (both M and N symbols stand for many or any number).¹⁵ Let us illustrate this constraint using the SUPPLY relationship in Figure 7.17.

Recall that the relationship set of SUPPLY is a set of relationship instances (s, j, p), where s is a SUPPLIER, j is a PROJECT, and p is a PART. Suppose that the constraint exists that for a particular project-part combination, only one supplier will be used (only one supplier supplies a particular part to a particular project). In this case, we place 1 on the SUPPLIER participation, and M, N on the PROJECT, PART participa-tions in Figure 7.17. This specifies the constraint that a particular ( j, p) combination can appear at most once in the relationship set because each such (PROJECT, PART) combination uniquely determines a single supplier. Hence, any relationship instance (s, j, p) is uniquely identified in the relationship set by its ( j, p) combination, which makes ( j, p) a key for the relationship set. In this notation, the participations that have a 1 specified on them are not required to be part of the identifying key for the relationship set. If all three cardinalities are M or N, then the key will be the combination of all three participants.

The second notation is based on the (min, max) notation displayed in Figure 7.15 for binary relationships. A (min, max) on a participation here specifies that each entity is related to at least min and at most max relationship instances in the relation-ship set. These constraints have no bearing on determining the key of an n-ary relationship, where n > 2, but specify a different type of constraint that places restrictions on how many relationship instances each entity can participate in.