Finite Differences | Numerical Methods - Relations between the operators Δ, ∇ and E | 12th Business Maths and Statistics : Chapter 5 : Numerical Methods
Chapter: 12th Business Maths and Statistics : Chapter 5 : Numerical Methods
Relations between the operators Δ, ∇ and E
Relations between the operators Δ, ∇ and E:
1. Δ ≡ E −1
Proof: From the definition
of Δ we know that
Δ f (x) = f (x + h ) − f (x) and
E[ f (x )] = f (x + h)
where h is the interval of difference.
Δ f (x) = f (x + h ) − f (x)
Δ f (x) = Ef (x ) − f (x)
⇒ Δ f (x) = (E −1) f (x)
Δ ≡ E −1
∴ E ≡
1 + Δ
2. Δ E ≡ Δ E
Proof:
E(Δf(x)) = E[f(x+h)- f(x)]
= E f(x+h) - E f(x)
= f(x+2h) - f(x+h)
=Δf(x+h)
=ΔEf(x)
ΔE ≡ ΔE
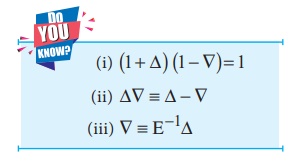
3. ∇≡ E −1 / E
∇f (x) = f (x) - f (x-h)
= f (x) – E-1f (x)
= (1- E-1) f (x)
∇ ≡ (1- E-1)
∇ ≡ 1 – 1/E
Hence ∇ ≡ [E – 1]/E
Related Topics