Example Solved Problems with Answer, Solution, Formula - LagrangeŌĆÖs interpolation formula | 12th Business Maths and Statistics : Chapter 5 : Numerical Methods
Chapter: 12th Business Maths and Statistics : Chapter 5 : Numerical Methods
LagrangeŌĆÖs interpolation formula
LagrangeŌĆÖs interpolation formula
The NewtonŌĆÖs forward and backward interpolation formulae can be
used only when the values of x are at equidistant. If the values of x
are at equidistant or not at equidistant, we use LagrangeŌĆÖs interpolation
formula.
Let y = f( x) be a function such that f ( x) takes the values y0
, y1 , y2 ,......., yn corresponding to x= x0
, x1, x2 ..., xn That is yi = f(xi),i
= 0,1,2,...,n . Now, there are (n + 1) paired values (xi, yi),i = 0, 1, 2, ..., n and hence
f ( x) can be represented by a polynomial function of degree n in x.
Then the LagrangeŌĆÖs formula is

Example 5.22
Using LagrangeŌĆÖs interpolation formula find y(10) from the
following table:

Solution:
Here the intervals are unequal. By LagrangeŌĆÖs interpolation
formula we have
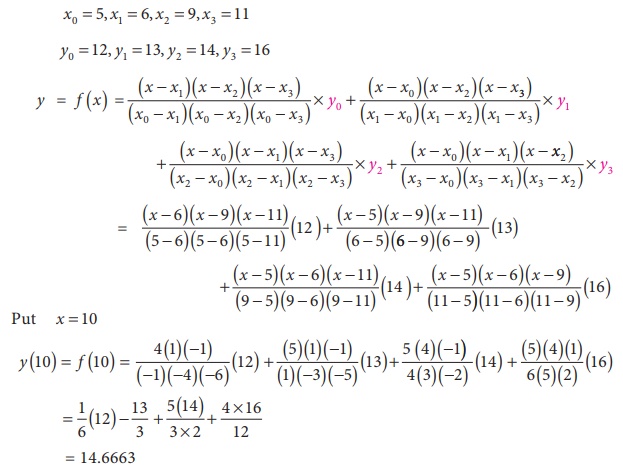
Related Topics