Numerical Methods - Graphical and Algebraic method of Interpolation: Solved Example Problems | 12th Business Maths and Statistics : Chapter 5 : Numerical Methods
Chapter: 12th Business Maths and Statistics : Chapter 5 : Numerical Methods
Graphical and Algebraic method of Interpolation: Solved Example Problems
Example 5.12
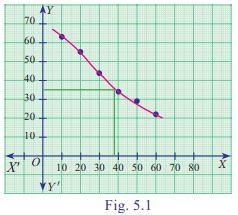
Using graphic method, find the value of y when x = 38 from the following data:

Solution:
From the graph in Fig. 5.1 we find that for x = 38, the value of y is equal to 35
Example 5.13
Using NewtonŌĆÖs formula for interpolation estimate the population
for the year 1905 from the table:

Solution:
To find the population for the year 1905 (i.e) the value of y at x
= 1905
Since the value of y is required near the beginning of the table,
we use the NewtonŌĆÖs forward interpolation formula.
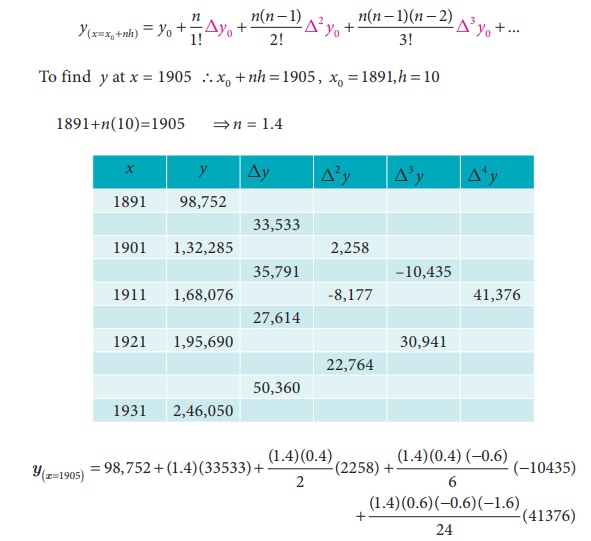
=
98,752 + 46946.2 + 639.8 + 584.36 + 1390.23
=
1,48,312.59
=
1,48,313
Example 5.14
The values of y =
f ( x)for x = 0,1,2, ...,6 are given
by

Estimate the value of y (3.2) using forward interpolation
formula by choosing the four values that will give the best approximation.
Solution:
Since we apply the forward interpolation formula, last four values
of f(x) are taken into consideration
(Take the values from x = 3).
The forward interpolation formula is

Example 5.15
From the following table find the number of students who obtained
marks less than 45.

Solution:
Let x be the marks and y be the number of students
By converting the given series into cumulative frequency
distribution, the difference table is as follows.

Example 5.16
Using appropriate interpolation formula find the number of
students whose weight is between 60 and 70 from the data given below

Solution:
Let x be the weight and y be the number of students.
Difference table of cumulative frequencies are given below.

Let
us calculate the number of students whose weight is below 70. For this we use
forward difference formula.
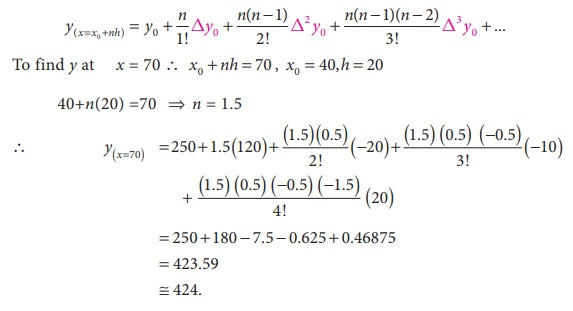
Number
of students whose weight is between
60
and 70 = y(70) ŌłÆ y(60) = 424 ŌłÆ 370 = 54
Example 5.17
The population of a certain town is as follows

Using appropriate interpolation formula, estimate the population during the period 1946.
Solution:

Here
we find the population for year1946. (i.e) the value of y at x=1946. Since the
value of y is required near the beginning of the table, we use the NewtonŌĆÖs
forward interpolation formula.

=
20 + 2 - 0.125 + 0.0625 ŌłÆ 0.24609
=
21.69 lakhs
Example 5.18
The following data are taken from the steam table.

Find the pressure at temperature t = 1750
Solution:
Since the pressure required is at the end of the table, we apply
Backward interpolation formula. Let
temperature be x and the pressure be y.

Example 5.19
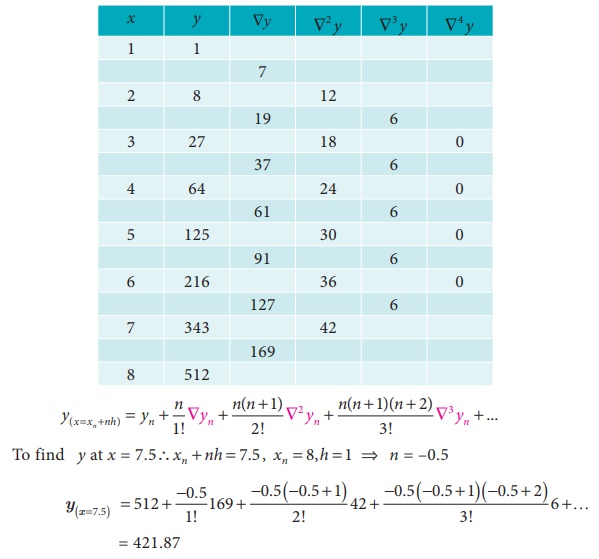
Calculate the value of y when x = 7.5 from the table given below

Solution:
Since the required value is at the end of the table, apply
backward interpolation formula.
Example 5.20
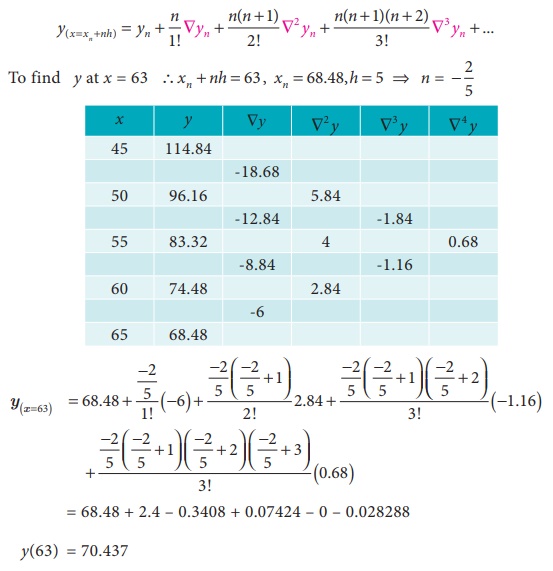
From the following table of half- yearly premium for policies
maturing at different ages. Estimate the premium for policies maturing at the
age of 63.

Solution:
Let age = x and premium = y
To find y at x = 63. So apply NewtonŌĆÖs backward interpolation
formula
Example 5.21
Find a polynomial of degree two which takes the values

Solution:
We will use NewtonŌĆÖs backward interpolation formula to find the
polynomial.

Related Topics