Numerical Methods - Finite Differences: Solved Example Problems | 12th Business Maths and Statistics : Chapter 5 : Numerical Methods
Chapter: 12th Business Maths and Statistics : Chapter 5 : Numerical Methods
Finite Differences: Solved Example Problems
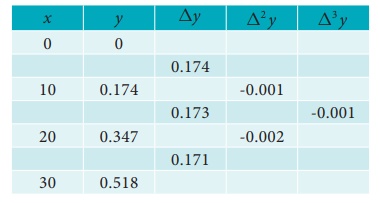
Example 5.1
Construct a forward difference table for the following data

Solution:
The Forward difference table is given below
Example 5.2
Construct a forward difference table for y = f(x)
= x 3 +
2x + 1 for x =
1,2,3,4,5
Solution:
y = f(x) = x3 + 2 x + 1 for x =1,2,3,4,5
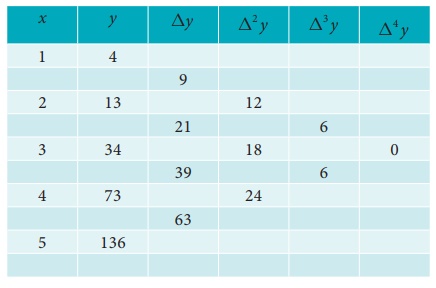
Example 5.3
By constructing a difference table and using the second order
differences as constant, find the sixth term of the series 8,12,19,29,42ŌĆ”
Solution:
Let
k be the sixth term of the series in the difference table
First
we find the forward differences.
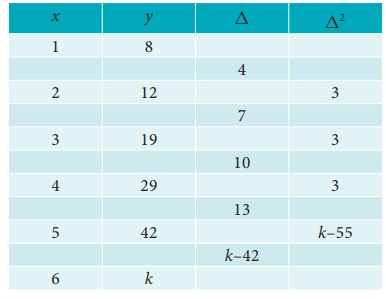
Given
that the second differences are constant
Ōł┤ k ŌĆō 55 = 3
k = 58
Ōł┤ the sixth term of the series is 58
Example 5.4
Find (i) Ōłåeax (ii) Ōłå2ex (iii) Ōłålogx
Solution:
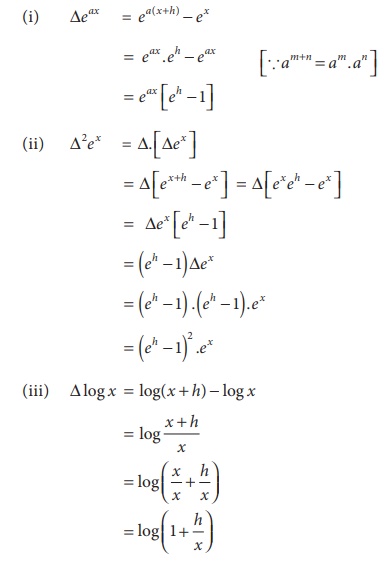
Example 5.5
Evaluate 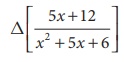 by taking ŌĆś1ŌĆÖ as the interval of differencing.
by taking ŌĆś1ŌĆÖ as the interval of differencing.
Solution:

Example 5.5
Evaluate 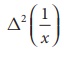 by taking ŌĆś1ŌĆÖ as the interval of differencing.
by taking ŌĆś1ŌĆÖ as the interval of differencing.
Solution:

Example 5.7
Prove that f(4) = f(3) + Δf(2) + Δ2f(1)
+ ╬ö3f(1) taking ŌĆś1ŌĆÖ as the interval of differencing.
Solution:
We know that f(4) - f(3) = Δ f(4)
f(4) - f(3) = Δ f(3)
= Δ [ f(2) + Δf(2) ]
i.e.[ f(3) - f(2) = Δf(2) ]
= Δ f(2) + Δ2f(2)
= Δ f(2) + Δ2[f(1)+
Δf(1)]
f(4) = f(3) + Δf(2) + Δ2 f(1) + Δ3 f(1)
Example 5.8
Given U0 =1, U1 =11, U2 =21, U3
=28 and U4 =29 find Δ4U0
Solution:
Δ4U0 = (E-1) 4U0

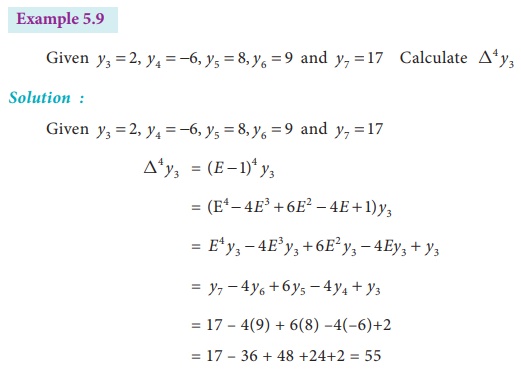
Related Topics