Methods of interpolation

Methods of interpolation

There are two methods for interpolation. One is Graphical method and the other one is algebraic method.

1. Graphical method

We are given the ‘n’ values of x and the corresponding values of y for given function y = f (x) . we plot these n observed points ( x_i , y_i ),i = 1,2,3.... and draw a free hand curve passing through these plotted points. From the graph so obtained, we can find out the value of y for any intermediate value of x. There is one drawback in the graphic method which states that the value of y obtained is the estimated value of y. The estimated value of y differs from the actual value of y.

Example 5.12

Using graphic method, find the value of y when x = 38 from the following data:

Solution:

From the graph in Fig. 5.1 we find that for x = 38, the value of y is equal to 35

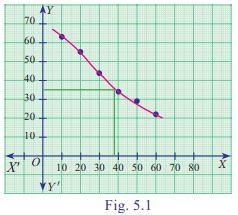
Steps in Graphic method:

Take a suitable scale for the values of x and y, and plot the various points on the graph paper for given values of x and y.

Draw a suitable curve passing through the plotted points.

Find the point corresponding to the value x = 38 on the curve and then read the corresponding value of y on the y- axis, which will be the required interpolated valu

2. Algebraic method

Newton’s Gregory forward interpolation formula (or) Newton’s forward interpolation formula (for equal intervals).

Let y = f ( x) denote a polynomial of degree n which takes (n + 1) values. Let them be y ₀ , y₁ , y ₂ ,... y_n corresponding to the values x , x ,... xn respectively.

The values of (x₀, x₁, x₂,….. x_n) are at equidistant.

(i.e.) x₁=x₀+h, x₂=x₀+2h, x₃=x₀+3h,……. X_n=x₀+nh,

Then the value of f(x) at x = x₀+nh is given by

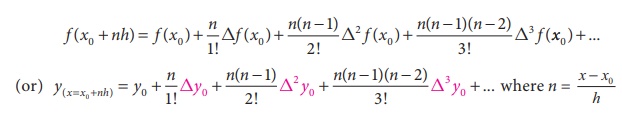
Newton’s Gregory backward interpolation Formula.

Note

Newton’s forward interpolation formula is used when the value of y is required near the beginning of the table. 

Newton’s forward interpolation formula cannot be used when the value of y is required near the end of the table. For this we use another formula, called Newton’s Gregory backward interpolation formula.

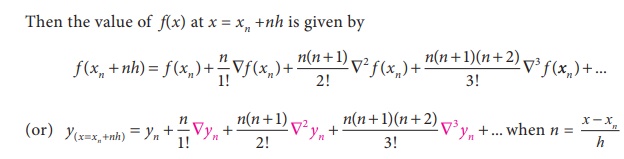
Note

Newton’s backward interpolation formula is used when the value of y is required near the end of the table.