Forward Difference Operator(∆)

Forward Difference Operator(∆ ):

Let y = f(x) be a given function of x. Let y ₀ , y₁ , y ₂ , ….. , y_n be the values of y at = x ₀ , x₁ , x ₂ ,•, x_n respectively. Then y₁ − y ₀ , y ₂ − y₁, y ₃ − y ₂ , …, y _n − y_n−1 are called the first (forward) differences of the function y. They are denoted by Δy ₀ , Δy₁ , Δy ₂ ,..., Δy_n−1 respectively.

(i.e) Δy ₀ = y₁ − y ₀ , Δy₁ = y ₂ − y₁, Δy ₂ = y₃ − y ₂ ,..., Δy_{n −1} = y _n − y_n−1

In general, Δy _n = y_n+1 − y _n , n = 0,1,2,3,...

The symbol Δ is called the forward difference operator and pronounced as delta.

The forward difference operator ∆ can also be defined as Df ( x) = f ( x + h ) − f ( x), h is the equal interval of spacing.

Proof of these properties are not included in our syllabus:

Properties of the operator Δ :

Property 1: If c is a constant then Δc = 0

Proof: Let f (x) = c

∴ f ( x + h ) = c (where ‘h’ is the interval of difference)

Δf ( x) = f ( x + h ) − f ( x)

Δc = c − c = 0

Property 2: Δ is distributive i.e. Δ ( f (x) + g (x)) = Δ f (x) + Δ g (x)

Proof: Δ[f (x) + g (x)] = [f (x + h ) + g(x + h) ] – [f (x)+ g (x)]

= f (x + h ) + g(x + h) − f (x) − g (x)

= f (x + h ) − f (x )+ g(x + h) − g (x)

= Δ f (x) + Δ g (x)

Similarly we can show that Δ [f ( x) − g ( x)] = f (x) − Δ [g ( x)]

In general, Δ[ f₁ (x) + f ₂ (x)...... + f _n (x) ] = Δ f₁ (x)+ Δ f ₂ (x) + .... + Δ f _n (x)

Property 3: If c is a constant then Δ c f ( x ) = c Δ f ( x)

Proof: Δ [c f (x)] = c f ( x + h) − c f ( x)

= c [ f (x + h) − f (x)]

= c Δ f (x)

Results without proof

1.        If m and n are positive integers then Δ ^m . Δ ⁿ f (x) = Δ ^{m +n} f (x)

2.        Δ[ f (x) g (x) ] = f (x) g (x) + g (x) Δ f (x)

3.         

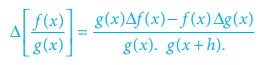
The differences of the first differences denoted by Δ²y₀, Δ²y₁, …., Δ²y_n, are called second differences, where

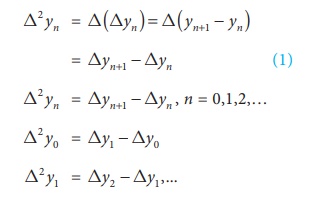
Similarly the differences of second differences are called third differences.

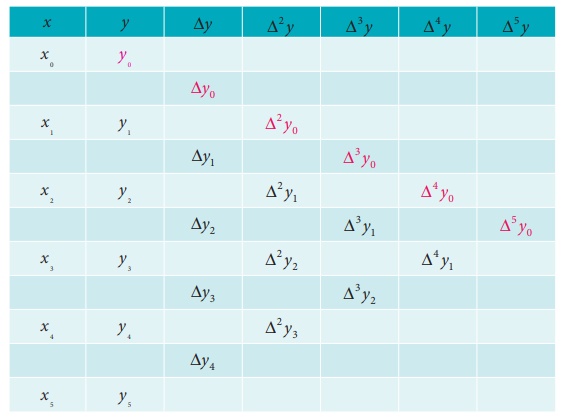
It is convenient to represent the above differences in a table as shown below.

Forward Difference Table for y :

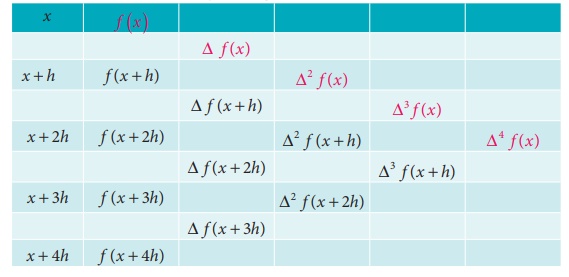
The forward difference table for f(x) is given below.