Regenerative Brayton Cycle

REGENERATIVE BRAYTON CYCLE

The temperature of the exhaust gases of simple gas turbine is higher than the temperature of air after compression. If the heat energy in the exhaust gases instead of getting dissipated in the atmosphere is used in heating air after compression, it will reduce the energy requirement from the fuel, thereby increasing the efficiency of the cycle

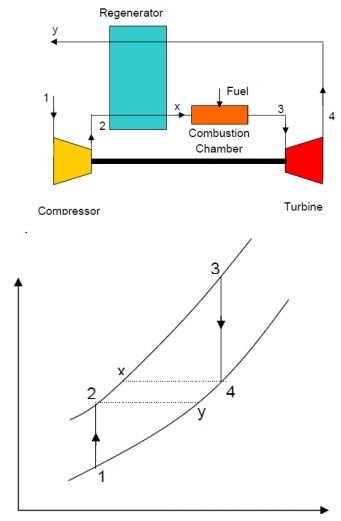
Air is drawn from the atmosphere into compressor and compressed isentropically to state 2. It is then heated at constant pressure in the regenerator to state x by hot burnt gases from the turbine. Since the temperature of air is increased before it reaches the combustion chamber, less amount of fuel will be required to attain the designed turbine inlet temperature of the products of combustion. After the combustion at constant pressure in the combustion chamber, the gas enters the turbine at state 3 and expands to state 4 isentropically. It then enters the counter-flow regenerator, where it gives up a portion of its heat energy to the compressed air from the compressor and leaves the regenerator at state y.

INTERCOOLING AND REHEATING

The addition of regenerator improves the ideal efficiency but does not improve the work ratio. The latter may be reduced by reducing the compressor work or increasing the turbine work.

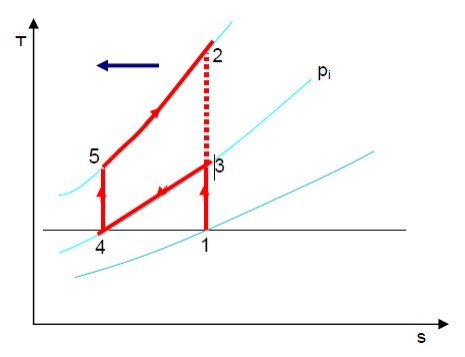
Consider the compressor work first. The curvature of the constant pressure lines on T-s diagram is such that the vertical distance between them reduces as we go towards the left (shown by the arrow). Therefore, further to the left the compression process 1-2 takes place, smaller is the work required to drive the compressor. State 1 is determined by the atmospheric pressure and temperature. But if the compression is carried out in two stages, 1-3 and 4-5 with the air is being cooled at constant intermediate pressure pi between the stages; some reduction of compression work can be achieved. The sum of temperature rises (T3 –T1) and (T5 –T4) will be clearly less than (T2 –T1). Ideally, it is possible to cool the air to atmospheric condition i.e. T4 = T1, and in this case Intercooling is complete.

4). A steam boiler generates steam at 30 bar, 300 °C at the rate of 2 kg/s. This steam is expanded isentropically in a turbine to a condenser pressure of 0.05 bar, condensed at constant pressure and pumped back to boiler.

a)    Find the heat supplied in the boiler per hour.

b)    Determine the quality of steam after expansion.

c)     What is the power generated by the turbine?

d)    Estimate the Ranking efficiency considering pump work.

Given Data:

p1 = 30 bar

p2 = 0.05 bar

T1 = 300°C

m = 2 kg / s

To find:

1.     Find the heat supplied in the boiler per hour (QS)

2.     Determine the quality of steam after expansion (x2)

3.     What is the power generated by the turbine (WT)

Estimate the Ranking efficiency considering pump work ( Ŋ)

Solution:

1.  Heat supplied in the boiler per hour (QS):     

Properties of steam from the steam table  

At 30 bar & 300°C                 

h1 = 2995.1 KJ/kg;         S1 = 6.542 KJ/kg K;      

At 0.05 bar          

hf2 = 137.8 KJ/kg; hfg2 = 2423.8 KJ/kg;      

Sf2 = 0.476 KJ/kg K;      Sfg2 = 7.920 KJ/kg K;    

Vf2 = 0.001005 m3/kg.           

1-2 = Isentropic expansion in the turbine  

S1 = S2 = 6.542 KJ/ kg K

S2= Sf2 + x2 ×Sfg2

6.542 = 0.476 + x2 × 7.92 = 0.766

Therefore, Quality of steam after expansion = 0.766 dry. h2 = hf2 + x2 ×hfg 2

= 137.81 + 0.766 × 2423.8

= 1994.43 KJ/kg.

h3 = hfg2 = 137.8 KJ/kg.

Considering the pump work, h4 –h3 = vf2 (p1 –p2)

h4 = h3 + vf2 (p1 –p2)

= 137.8 + 0.001005 × (30 - 0.05) × 102

= 140.81 KJ/kg.

Heat supplied in the boiler:

QS = m × (h1 –h4)

= 2 × (2995.1 –140.81)

= 5708.58 KJ/s

= 20.55 × 106 KJ /hr.

Power generated by the turbine:

WT = m × (h1 –h2)

= 2 × (2995.1 –1994.43)

= 2001.34 KW.

Rankine efficiency by the plant:

(h1 –h2) - (h4 –h3) / (h1 –h4)

= (2995.1 –1994.43) - (140.81 –137.8) / (2995.1 –140.81)

= 35 %

Result:

1.     Find the heat supplied in the boiler per hour (QS) = 20.55 × 106 KJ /hr

2.     Determine the quality of steam after expansion (x2) = 0.766 dry

3.     What is the power generated by the turbine (WT) = 2001.34 KW.

4.     Estimate the Ranking efficiency considering pump work ( Ŋ) = 35%