Chapter: Mechanical : Engineering Thermodynamics : Properties of a Pure Substance and Steam Power Cycle
Formation of Steam and Properties
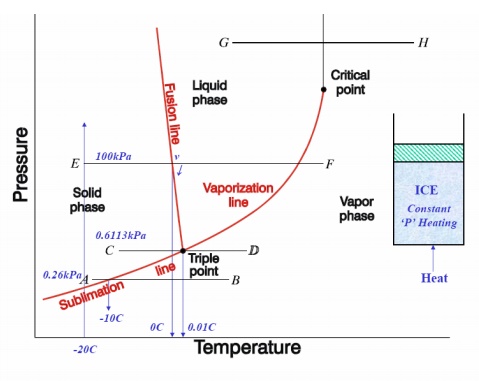
FORMATION OF STEAM AND PROPERTIES
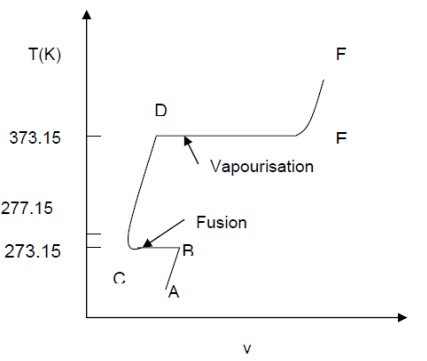
Imagine
unit mass of ice below the freezing point, enclosed in a cylinder by a piston
under a constant load of 1 atmosphere (1 atm. = 1.01325 bar = 101.325 kPa). If
heat is added to the cylinder while keeping the pressure constant, the
temperature rises and ice expands until a temperature of 273.15 K (00C) is
reached (AB) as shown in Fig. Further heating does not raise the temperature of
ice but causes a change to the liquid phase (BC). The change of phase occurs at
a constant temperature and by reduction of specific volume. The heat required
for this process is known as latent heat of fusion. Further
heating results in a rise of temperature of liquid and a further contraction in
volume until the temperature is about 40C and subsequent expansion until a
temperature of 373.15 K (1000C) is reached (point D). At this point a second
phase change occurs at constant temperature with a large increase in volume
until the liquid has been vaporised (point E). The heat required in this case
is called the latent heat of vaporisation. When vaporisation is
complete, the temperature rises again on heating (line EF). The heat
transferred to a substance while the temperature changes is sometimes referred
to as sensible heat. This constant pressure lines
are called isobars.
If
the pressure is reduced, there is a slight rise in the melting point and also
there is a marked drop in the boiling point of water and a marked increase in
the change in volume, which accompanies evaporation. When the pressure is
reduced to 0.006113 bar (0.6113 kPa), the melting point and boiling point
temperatures become equal and change of phase, ice-water-steam, are represented
by a single line. The temperature at which this occurs has been accepted
internationally as a fixed point for the absolute temperature scale and is by
definition 273.16 K. Only at this temperature and pressure of 0.6112 kPa, can
ice, water and steam coexists in thermodynamic equilibrium in a closed vessel
and is known as triple point. If the pressure is reduced further,
the ice, instead of melting, sublimes directly into steam.
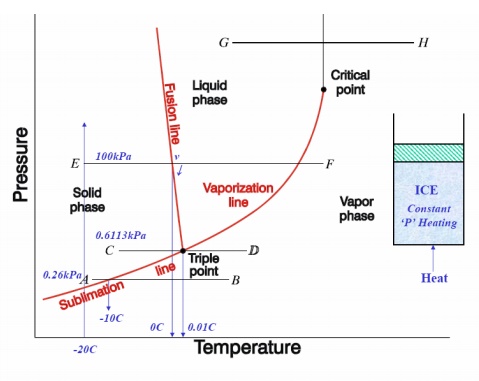
p-v, p-T, T-v, T-s, h-s DIAGRAMS
Consider now the
behaviour at pressure above atmospheric. The shape of the curve is similar to
that of the atmospheric isobar, but there is a marked reduction in the change
in volume accompanying evaporation. At a sufficiently high pressure, this
change in volume falls to zero and the horizontal portion of the curve reduces
to a point of inflexion. This is referred to critical point. The values
pressure and temperature of water at which critical point reached are
pc
= 221.2 bar = 22.12 MPa ; Tc = 647.3 K ; vc = 0.00317 m3/kg.
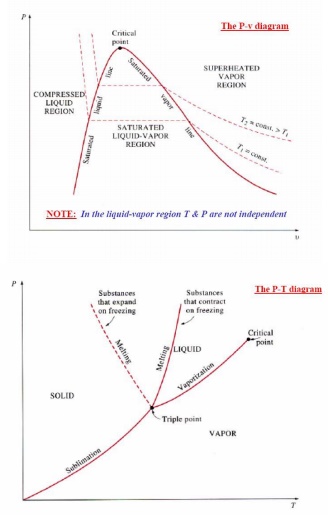
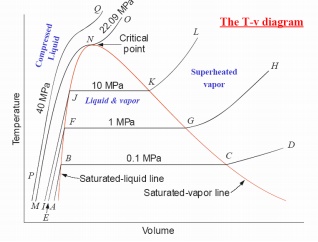
The pressure at which
liquid vaporises or condenses is called saturation pressure
corresponding to a given temperature. Alternately, the temperature at
which this phenomena occur is called saturation temperature
corresponding to the given pressure. A vapour in a state lying along the
saturated vapour line is also called dry saturated vapour and the
vapour lying right of this line is called superheated vapour.
DEFINITION AND
APPLICATIONS
•Saturation
temperature: Temperature at which a pure substance changes phase at
a
given pressure.
•Saturation
pressure: Pressure at which a pure substance changes phase at a given
temperature.
•Latent heat: The amount of
energy absorbed or released during a phase-change. Melting/freezing: Latent
heat of fusion.
Evaporation/condensation: Latent
heat of vaporization.
•Temperature at
which water starts boiling depends on the pressure => if the pressure
is fixed, so is the boiling temperature.
SLOVED PROBLEMS
1. A vessel of volume
0.04 m3 contains a mixture of saturated water and steam at a
temperature of 250°C. The mass of the liquid present is 9 kg. Find the
pressure, mass, specific volume, enthalpy, entropy and internal energy.
[April/May 2012,2015]
Given Data:
Volume, V = 0.04 m3
Temperature, T = 250°C
Mass, m = 9 kg
To find:
1) p, 2) m, 3) v, 4) h, 5) S,6) ΔU
Solution:
From the Steam tables
corresponding to 250°C, vf = v1 = 0.001251 m3/kg
vg = vs
= 0.050037 m3/kg p = 39.776 bar
Total volume occupied by the liquid,
V1 = m1 × v1
= 9
× 0.001251
= 0.0113
m3.
Total volume of the vessel,
V
= Volume of liquid + Volume of steam
= V1 + VS
0.4 =
0.0113 + VS
VS
= 0.0287 m3.
Mass of steam, ms = VS / vs
= 0.0287
/ 0.050037
= 0.574
kg.
Mass of mixture of liquid and steam, m = m1
+ ms
= 9
+ 0.574
= 9.574
kg.
Total specific volume of the mixture,
v =
= 0.04
/ 9.574
= 0.00418
m3 / kg.
We know that,
v
= vf + x vfg
0.00418 = 0.001251 + x (0.050037
–0.001251) x = 0.06
From Steam table corresponding to 250
°C, hf = 1085.8 KJ / kg
hfg
= 1714.6 KJ / kg
sf
= 2.794 KJ / kg K
sfg
= 3.277 KJ / kg K.
Enthalpy of mixture,
h =
hf + x hfg
= 1085.8
+ 0.06 × 1714.6
=
1188.67 KJ / kg Entropy of mixture,
s =
sf + x sfg
= 2.794
+ 0.06 × 3.277
=
2.99 kJ / kg K. Internal energy, u = h
–p v
= 1188.67
–39.776×102 × 0.00418
= 1172
KJ / kg.
Result:
1) p
= 39.776 bar
2) m
= 9.574 kg
3) v
= 0.00418 m3 / kg
4) h
= 1188.67 KJ / kg
5) S
= 2.99 KJ /kg K
6) ΔU=
1172 KJ / kg.
2). A steam
power plant uses steam at boiler pressure of 150 bar and temperature of 550°C
with reheat at 40 bar and 550 °C at condenser pressure of 0.1 bar. Find the
quality of steam at turbine exhaust, cycle efficiency and the steam rate.
[May/June 2014]
Given Data:
p1 = 150 bar
T1 = 550°C
p2 = 40 bar
T3 = 550 °C
p3 = 0.1 bar
To find:
1. The
quality of steam at turbine exhaust, (x4)
2. cycle
efficiency and
3. The
steam rate.
Solution:
1. The quality of steam at turbine
exhaust, (x4):
Properties of steam from steam tables at
150 bar & 550°C h1 = 3445.2 KJ/kg.
S1= 6.5125
KJ/kg K At 40 bar & 550°C
h3
= 3558.9 KJ/kg.
S3=
7.2295 KJ/kg K
At 40 bar
Tsat
= 250.3°C = 523.3 K
hf =1087.4 KJ/kg. hfg = 1712.9 KJ/kg.
Sf= 2.797 KJ/kg K Sfg= 3.272 KJ/kg
K
At 0.1 bar
hf =191.8 KJ/kg. hfg = 2392.9 KJ/kg.
Sf= 0.649 KJ/kg K Sfg= 7.502 KJ/kg K
1-2 = isentropic
S1
= S = 6.5125 KJ/kg K
S2
= Sg at 40 bar
Therefore,
Exit of HP turbine is superheat
Tsup
= 332°C
h2
= 3047.18 KJ/kg
S3
= Sg at 0.1 bar
Steam is at wet condition.
S4
= S3 = 7.2295 KJ/kg K
S4
= Sf4 + x4 Sfg4
7.2295
= 0.649 + x4 × 7.502
x4
= 0.877
h4
= hf4 + x4 hfg4
=
191.8 + 0.877 × 2392.9
h4
= 2290.37 KJ/kg K
2) Cycle efficiency:
D = (h1
–h2) + (h3 –h4) / (h1 –hf4) + (h3
–h2)
= (3445.2
–3047.15) + (3558.9 –2290.37) / (3445.2 –191.8) + (3558.9 –3047.18)
= 0.4426 × 100
= 44.26%
3) Steam rate:
= 3600
/ (h1 –h2) + (h3 –h4)
= 3600 / (3445.2 –3047.15) + (3558.9 –2290.37)
=
2.16 kg/Kw–hr.
Result:
1. The
quality of steam at turbine exhaust, (x4) = 0.877
2. cycle
efficiency = 44.26%
3. The
steam rate = 2.16 kg/Kw–hr.
3). Ten kg of water 45
°C is heated at a constant pressure of 10 bar until it becomes superheated
vapour at 300°C. Find the change in volume, enthalpy, internal energy and
entropy.
Given Data:
m= 10 kg
p1 = p2 = 10 bar
T2 = 300°C
To find:
1) Change
in volume,
2) Change
in Enthalpy,
3) Change
in Internal energy,
4) Change
in Entropy.
Solution:
From steam tables, corresponding to 45°C,
v1=vf1=0.001010 m3 /
kg; h1 = hf1
= 188.4 KJ/kg;
s1 = sf1 = 0.638 KJ/kg K
From steam tables, corresponding to 10 bar and
300°C,
h2 =
3052.1 KJ/kg; s2 = 7.125 KJ/kg K;
v2 = 0.258
m3 /kg;
Change
in Volume,2–v1) V
= m (v
= 10 (0.258 –0.001010)
= 2.5699 m3.
Change in
Enthalpy,2–1) h =
m (h
= 10
(3052.1 –188.4)
= 28637
KJ.
Change in
Entropy,2–s1) S =
m (s
= 10
(7.125 –0.638)
= 64.87
KJ/K.
Change in
Internal2–u1)
energy, U =
m (u
= m
[(h2 - h1) –(p2v2 –p1v1)]
= m
[(h2 - h1) –p1 (v2 –v1)
= 10
[(3052.1 –188.4) –1000 (0.258 –0.001010)]
= 26067.1
KJ.
Result:
1) Change in volume,
ΔV= 2.5699 m3.
2) Change in
Enthalpy,=h28637 KJ.
3) Change in
Internal energy, ΔU = 26067.1
KJ.
4) Change in
Entropy, ΔS = 64.87
KJ/K.
Related Topics