Refractometry: Theory

THEORY

Lorentz and Lorentz in 1880, introduced the terminology specific refraction or refractivity which may be expressed as :

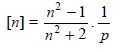                .............................(3)

where, n = Refractive index,

p = Density of the substance*

Hence, the specific refraction (Eq. 3) is considered to be a more useful property and is characteristic of the substance, being absolutely independent of temperature.

Molar Refractivity : 

Later on, a still more useful property termed as the molar refraction (or refrac-tivity) was introduced which could be expressed as follows :

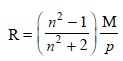             .............................................(4)

where, R = Molar refraction,

P = Density of the substance, and

M = Molecular weight.

Interestingly, both specific refraction [n] and molar refraction (R), being temperature independent, should have the same values for a given substance either in the solid, liquid or gaseous state, provided the molecular structure is unchanged.

Unit of Molar Refraction : 

As the refractive index is a dimensionless quantity, the units of molar refraction are simply those of molar volume, M/p i.e., cm³. mol^–1.

The molar refractivity is more or less an additive property.

Atomic Refractivities : 

Atomic refractivities may be attributed by virtue of :

(a) Structural features e.g., double bond, triple bond or nature of ring structure (3-member/4-member rings), and

(b) Individual atoms, e.g., H, C, Cl, Br, I and O. However, ‘O’ contributes different values for differ-ent groups, for instance : hydroxyl (—OH), carbonyl (—CO—) and ethereal (—O—) moieties.

A few representative atomic refractivities and bond contributions are given in Table 18.1 below :

Based on the atomic refractivities given in Table 18.1, it may be possible to calculate the molar refractivities of various pharmaceutical substances theoretically and compare the same with values found experimentally. A few typical examples are cited below :

(a) Acetone, CH₃COCH₃  [or C₃H₆O] :

R_C3H6O = 3 R_C + 6R_H + R_O

=3 × 2.418 + 6 × 1.100 + 2.211

=7.254 + 6.600 + 2.11 = 15.964

Calculated : R_{C 3 H 6O}  = 15.964 cm³ mol^–1

Experimental : R_{C 3 H 6O}  = 15.985 cm³ mol^–1

(b) Methyl Alcohol, CH₃OH [or CH₄O] :

R_{CH 3OH} ^{= R}C ^{+ 4R}H ^{+ R}O

                  = 2.418 + 4 × 1.100 + 1.525

                  = 2.418 + 4.400 + 1.525

                   = 8.343

Calculated : R_{CH 4O}  = 8.343 cm³ mol^–1

Experimental : R_{CH 4O}  = 8.296 cm³ mol^–1

(c) Chloroform CHCl₃ :

                  CHCl₃ ^{= R}_C ^{+ R}_H ^{+ 3R}_Cl

                  = 2.418 + 1.100 + 3 × 5.967

                  = 2.418 + 1.100 + 17.901

                  = 21.419

Calculated : R_CHCl3 = 21.419 cm³ mol^–1

Experimental : R_CHCl3 = 21.393 cm³ mol^–1.