Refractometry: Instrumentation

INSTRUMENTATION

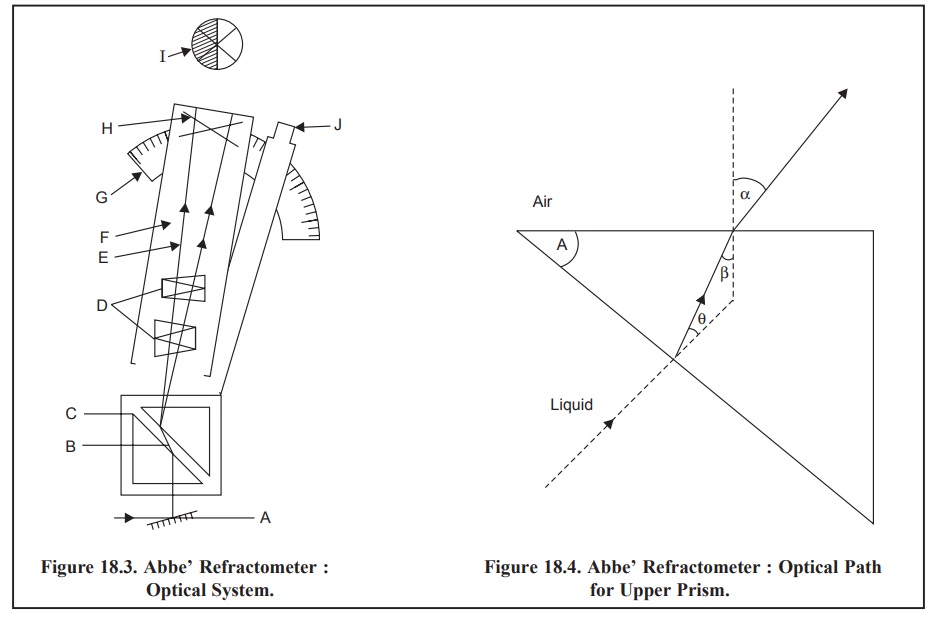
In Figure 18.3, the optical system of Abbe’ Refractometer has been shown based on the critical angle principle.

The various parts in Figure 18.3, are stated as below :

A = Mirror ;                                                 

F = Telescope ;

B = Liquid (Sample) ;                                  

G = Scale ;

C = Prism box ;                                           

H = Cross hair ;

D = Amici Prisms ;                                       

I = Field of view ;

E = Critical ray ;                                          

J = Eye-piece for reading scale ;

Procedure : 

The liquid whose RI is to be determined is placed between the two prisms (B). The upper face of the lower prism has a ground surface so as to diffuse the light rays in every possible direction. The rays passing from the liquid to the upper prism undergoes refraction in the normal manner, thereby providing a bright field in the eye-piece. The critical ray is originated by virtue of the rays that strike the liquid glass interface at the grazing incidence. As an outcome of these combined effects the ‘field of view’ is represented as a distinct dark and light area having a sharp dividing line.

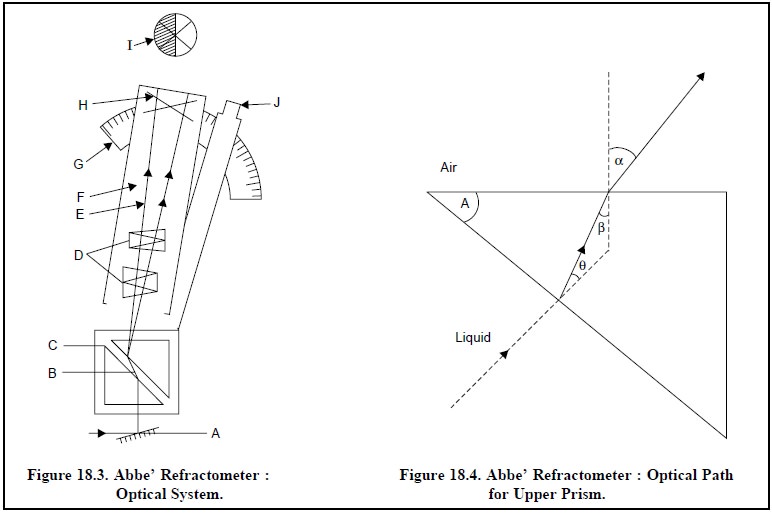
Fig. 18.4, designates the optical path for the upper prism in Abbe’ Refractometer. When a ray of light passes from the liquid medium and enters the upper prism, it gets refracted by an angle θ between the lower face of the prism and the normal, an angle β between the emerging refracted ray at the upper face and the normal, and finally an angle α between the reflected ray at the upper face and the normal. Thus, we have :

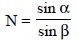                 .........................(a)

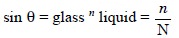 ................................(b)

where, N = Refractive index of the prism compared to air, and

n= Refractive index of the liquid (air to liquid)

and A = β + θ

or    θ = A – β             ....................(c)

From Eq. (b) we have :

n = N sin θ           ....................(d)

Putting the value of θ from Eq. (c) in Eq. (d), we have :

n = N sin (A – β)

or    n = N sin A cos β – N cos A sin β              .......................(e)

As we know       sin² β + cos² β = 1                 ...............................(f)

From Eq. (a) we have :

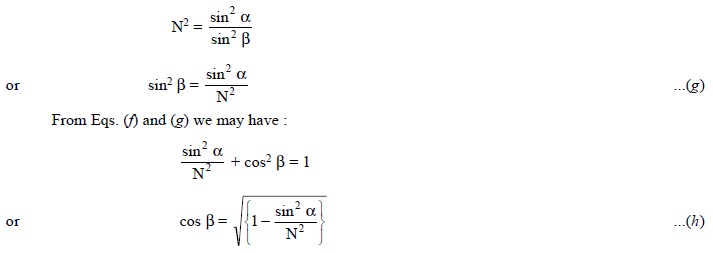
Substituting the value of cos  β  from Eq. (h) in Eq. (e) and also sin β = sin α/N from Eq. (a) we have :

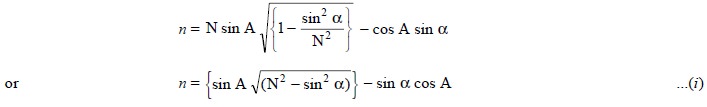
Now, based on the two constants, viz., A and N, for a specific prism and a measurable angle α it is convenient to determine the refractive index of the liquid n relative to air from Eq. (i). With the help of the Abbe’ refractometer the angle α lying between the normal and the critical ray emerging from the upper surface of the prism may be measured. By the aid of the two constants A and N (for a particular prism) the angle α has been converted into the refractive index directly and the scale of the instrument has been duly calibrated and printed accordingly.

The telescope (F) of the Abbe’ refractometer is fixed (Figure 18.3) and the prism box (C) is directly attached to the scale. When C is made to rotate gradually the critical ray (E) falls on the cross hair (H) of the telescope (F). At this juncture the value of the refractive index of the liquid (n) can be measured directly from the scale (G).

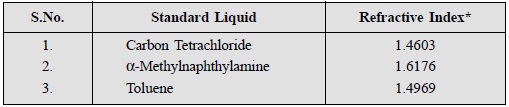
It is, however, important to mention here that the calibration of Abbe’s refractometer may be checked periodically by making use of standard liquids whose refractive index are stated in the European Pharmacopoea (as Reference Liquids).

For instance