Reduction of State and Flow Tables

REDUCTION OF STATE AND FLOW TABLES

The procedure for reducing the number of internal states in an asynchronous sequential circuit resembles the procedure that is used for synchronous circuits.

ü Implication Table and Implied State

The state-reduction procedure for completely specified state tables is based on an algorithm that combines two slates in a slate table into one as long as they can be shown to be equivalent. Two states are equivalent if, for each possible input, they give exactly the same output and go to the same next states or to equivalent next states.

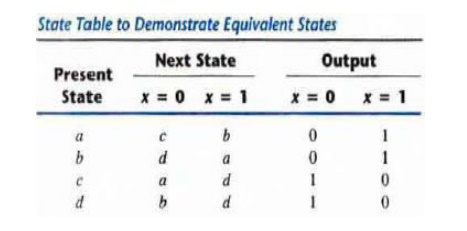
Consider for example the state table shown in above table. The present states a and b have the same output for the same input. Their next states are c and d for x = 0 and b and a for x = 1. If we can show that the pair of states (c, d) are equivalent, then the pair of states (a , b) will also be equivalent, because they will have the same or equivalent next states. When this relationship exists, we say that (a. b) imply (c, d) in the sense that if a and b are equivalent then r and d have to be equivalent. Similarly, from the last two rows of above table, we find that the pair of stales (c, d) implies the pair of states (a, b). The characteristic of equivalent states is that if (a, b) imply (c, d) and (c, d) imply (a, b), then both pairs of states are equivalent that is, a and b are equivalent, and so are c and d. As a consequence, the four rows of table can be reduced to two rows by combining a and b into one state and c and d into a second state.

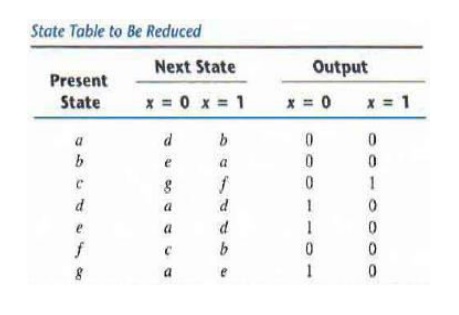
The implication table is shown in Fig. On the left side along the vertical are listed all the states defined in the state table except the first and across the bottom horizontally are listed all the states except the last. The result is a display of all possible combinations of two stares with a square placed in the intersection of a row and a column where the two states can be tested for equivalence. Two states having different outputs for the same input are not equivalent.

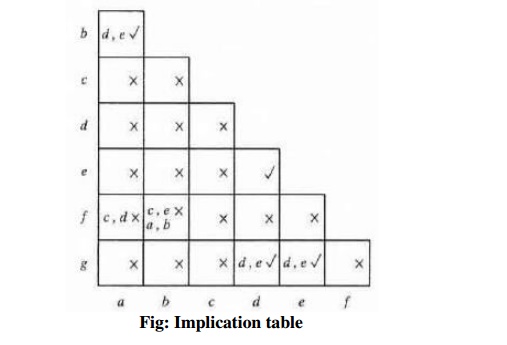
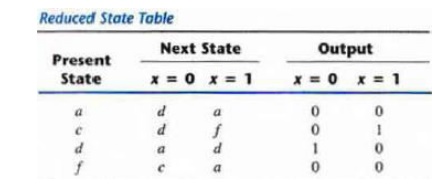
Two states that are not equivalent are marked with a cross [X] in the corresponding square whereas their equivalence is recorded with a check mark(‘Dik’). Some of the squares have entries of implied states that must be investigated further to determine whether they are equivalent. Thus table can be reduced from seven states to four one for each member of the preceding partition. The reduced state table is obtained by replacing state b by a and states e and g by d and it is shown below,

ü    Merging of the Flow Table

Incompletely specified states can be combined to reduce the number of state in the flow table. Such stares cannot be called equivalent because the formal definition of equivalence requires that all outputs and next states be specified for all inputs. Instead, two incompletely specified states that can be combined are said to be Compatible. The process that must be applied in order to find a suitable group of compatibles for the purpose of merging a flow table can be divided into three steps:

1.                 Determine all compatible pairs by using the implication table.

2.                 Find the maximal compatibles with the use of a merge r diagram.

3.                 Find a minimal collection of compatibles that covers all the states and is closed.

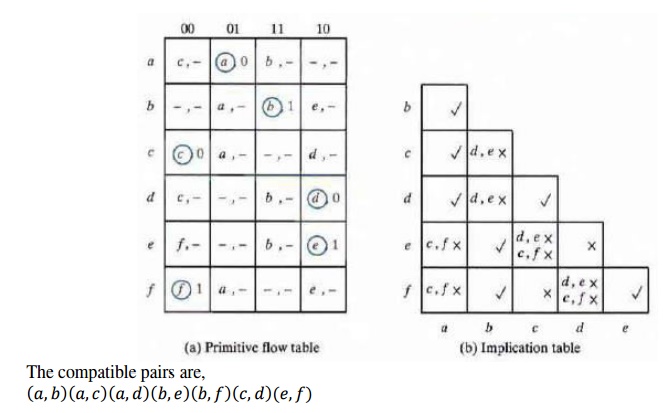
ü Compatible Pairs-The entries in each square of primitive flow table represent the next state and output The dashes represent the unspecified states or outputs. The implication table is used to fmd compatible states just as it is used to find equivalent stales in the completely specified case. The only difference is that, when comparing rows, we are at liberty to adjust the dashes to fit any desired condition.

ü    Maximal Compatibles

The maximal compatible is a group of compatibles that contains all the possible combinations of compatible states. The maximal compatible can be obtained from a merger diagram. The merger diagram is a graph in which each state is represented by a dot placed along the circumference of a circle. Lines are drawn between any two corresponding dots that form a compatible pair. All possible compatibles can be obtained from the merger diagram by observing the geometrical patterns in which states are connected to each other. An isolated dot represents a state that is not compatible with any other state. A line represents a compatible pair. A triangle constitutes a compatible with three states.

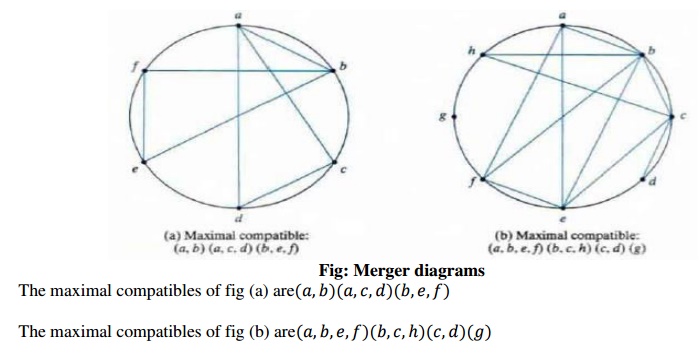
The maximal compatibles of fig (a) are

The maximal compatibles of fig (b) are

Closed-Covering Condition

The condition that must be satisfied for merging rows is that the set of chosen compatibles must cover all the states and must be closed. The set will cover all the states if it includes all the states of the original state table. The closure condition is satisfied if there are no implied states or if the implied states are included within the set. A closed set of compatibles that covers all the states is called a closed covering.

Example: