Design Procedure of Asynchronous Sequential circuits

DESIGN PROCEDURE

There are a number of steps that must be carried out in order to minimize the circuit complexity and to produce a stable circuit without critical races. Briefly, the design steps are as follows:

Ø Obtain a primitive flow table from the given specification.

Ø Reduce the flow table by merging rows in the primitive flow table.

Ø Assign binary states variables to each row of the reduced flow table to obtain the transition table.

Ø Assign output values to the dashes associated with the unstable states to obtain the output maps.

Ø Simplify the Boolean functions of the excitation and output variables and draw the logic diagram.

The design process will be demonstrated by going through a specific example:

Design Example – Specification

Design a gated latch circuit with two inputs, G (gate) and D (data), and one output Q. The gated latch is a memory element that accepts the value of D when G = 1 and retains this value after G goes to 0. Once G = 0, a change in D does not change the value of the output Q.

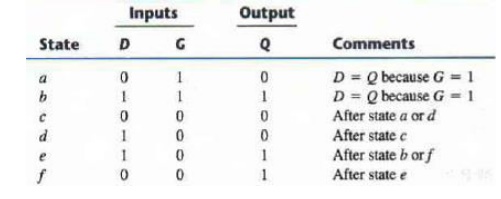
ü Step 1: Primitive Flow Table

A primitive flow table is a flow table with only one stable total state in each row. The total state consists of the internal state combined with the input.

To derive the primitive flow table, first a table with all possible total states in the system is needed:

Each row in the above table specifies a total state; the resulting primitive table for the gated latch is shown below:

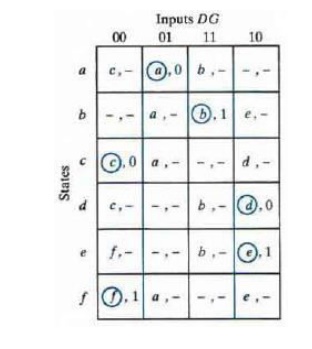
First, we fill in one square in each row belonging to the stable state in that row. Next recalling that both inputs are not allowed to change at the same time, we enter dash marks in each row that differs in two or more variables from the input variables associated with the stable state. Next we find values for two

more squares in each row. The comments listed in the previous table may help in deriving the necessary information. A dash indicates don’t care conditions.

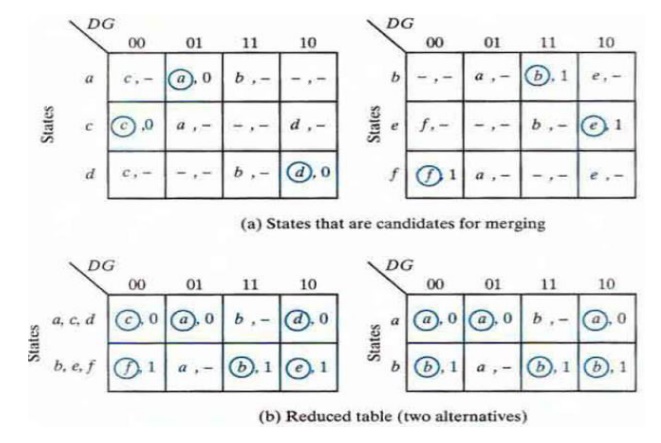
ü Step 2: Reduction of the Primitive Flow Table

The primitive flow table can be reduced to a smaller number of rows if two or more stable states are placed in the same row of the flow table. The simplified merging rules are as follows:

Ø Two or more rows in the primitive flow table can be merged into one if there are non- conflicting states and outputs in each of the columns.

Ø Whenever, one state symbol and don’t care entries are encountered in thethesamestate column, is listed in the merged row.

Ø If the state is circled in one of the rows, it is also circled in the merged row.

Ø The output state is included with each stable state in the merged row.

Now apply these rules to the primitive flow table shown previously. To see how this is done the primitive flow table is separated into two parts of three rows each:

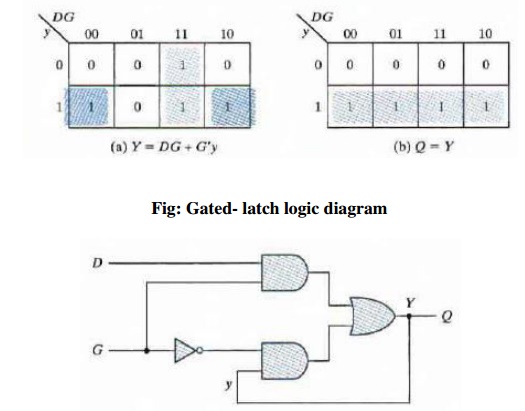
ü Step 3: Transition table and logic diagram

The assignment of distinct binary value to each state converts the flow table into a transition table. In the general case, a binary state assignment must be made to ensure that the circuit will be free of critical races. There can be no critical races in a two-row flow table; therefore, we can finish the design of the gated latch. Assigning 0 to state a and 1 to state b in the reduced flow table, we obtain the transition table. The transition table is, in effect, a map for the excitation variable Y. The simplified Boolean function for Y is then obtained from the map.

 There are two don’t-care outputs in the final reduced flow table. Alternatively, if we replace the don’tcare by 1 when y = 1 and DG= 01, the map reduces to Q = Y. If we assign the other possible values to the don't -care outputs. We can make output Q equal to y.

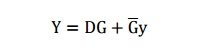
ü Step 4: Assigning Outputs to Unstable States

The stable states in a flow table have specific output values associated with them. The unstable states have unspecified output entries designated by a dash. The output values for the unstable states must be chosen so that no momentary false outputs occur when the circuit switches between stable states. This means that if an output variable is not supposed to change as the result of a transition. then an unstable state that is a transient state between two stable states must have the same output value as the stable states.

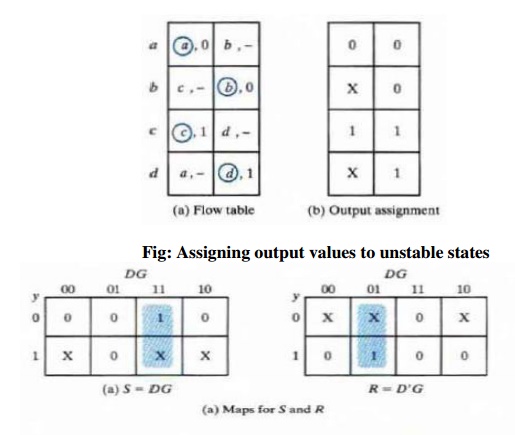
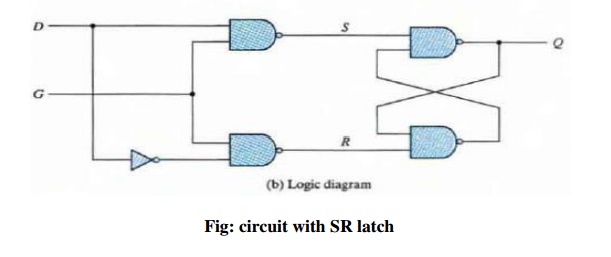
If an output variable is 10 change value as a result of a change in state, then this variable is assigned a don’ -tcare condition. If a 0 is entered as the output value for the unstable state c, then the change in the output variable will not take place until the end of the transition. If a 1 is entered, the change will take place at the start of the transition, since it makes no difference, Reduction of State and Flow tables when the change in output occurs, we place a don't-care entry for the output associated with unstable state.