Analysis of Asynchronous Sequential circuits

ASYNCHRONOUS SEQUENTIAL CIRCUITS

PRE-REQUISITE DISCUSSION

The communication of two units, with each unit having its own independent clock, must be done with asynchronous circuits.

·        Do not use clock pulses. The change of internal state occurs when there is a change in the input variable.

·        Their memory elements are either unclocked flip-flops or time-delay elements.

·        They often resemble combinational circuits with feedback.

·        Their synthesis is much more difficult than the synthesis of clocked synchronous sequential circuits.

·        They are used when speed of operation is important.

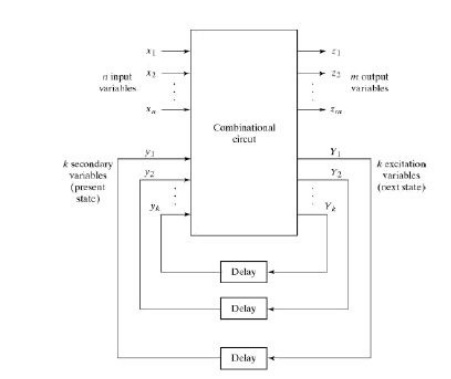
ANALYSIS PROCEDURE

The analysis of asynchronous sequential circuits proceeds in much the same way as that of clocked Synchronous sequential circuits. From a logic diagram, Boolean expressions are written and then transferred into tabular form.

ü Transition Table

The analysis of the circuit starts by considering the excitation variables (Y1 and Y2) as outputs and the secondary variables (y1 and y2) as inputs.

The circuit has four stable total states, =000,011,110, and 101 and four unstable total states-001,010,111 and 100.

The state table of the circuit is shown below:

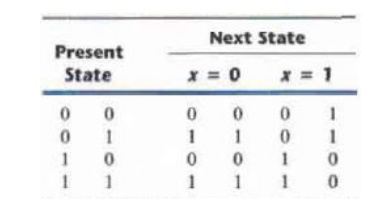
This table provides the same information as the transition table.

ü Flow table

In a flow table the states are named by letter symbols. Examples of flow tables are as follows:

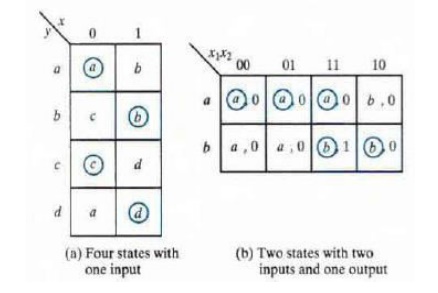
In order to obtain the circuit described by a flow table, it is necessary to assign to each state a distinct value.

This assignment converts the flow table into a transition table. This is shown below,

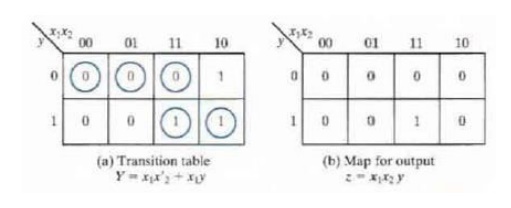
The resulting logic diagram is shown below,

ü Race Conditions

A race condition exists in an asynchronous circuit when two or more binary state variables change value in response to a change in an input variable. When unequal delays are encountered, a race condition may cause the state variable to change in an unpredictable manner.

If the final stable state that the circuit reaches does not depend on the order in which the state variables change, the race is called a noncritical race. Examples of noncritical races are illustrated in the transition tables below:

The transition tables below illustrate critical races:

Fig: Examples of critical races

Races can be avoided by directing the circuit through a unique sequence of intermediate unstable states. When a circuit does that, it is said to have a cycle. Examples of cycles are:

ü Stability Considerations

An asynchronous sequential circuit may become unstable and oscillate between unstable states because of the presence of feedback. The instability condition can be detected from the transition table. Consider the following circuit:

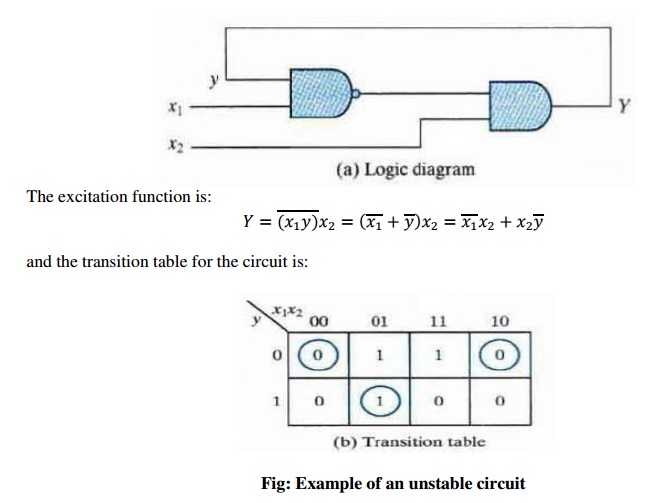
Those values of Y that are equal to y are circled and represent stable states. When the input x1x2 is 11, the state variable alternates between 0 and 1 indefinitely.

CIRCUITS WITH SR LATCHES

The SR latch is used as a time-delay element in asynchronous sequential circuits. The NOR gate SR latch and its truth table are:

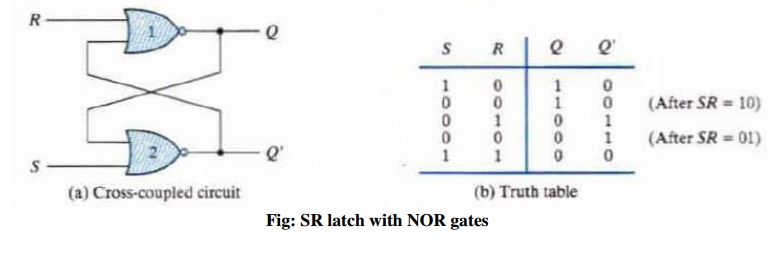
Fig: SR latch with NOR gates

The feedback is more visible when the circuit is redrawn as:

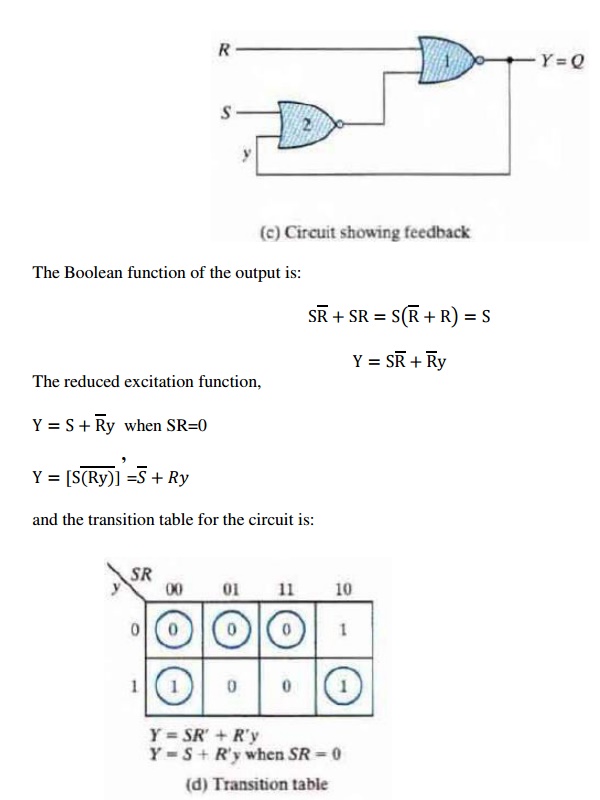
The behavior of the SR latch can be investigated from the transition table. The condition to be avoided is that both S and R inputs must not be 1 simultaneously. This condition is avoided when SR = 0 (i.e., ANDing of S and R must always result in 0). When SR = 0 holds at all times, the excitation function

derived previously:

Fig: SR latch with NAND gates

The condition to be avoided here is that both S and R not be 0 simultaneously which is satisfied when

S′R′ = 0.

ANALYSIS EXAMPLE

Consider the following circuit:

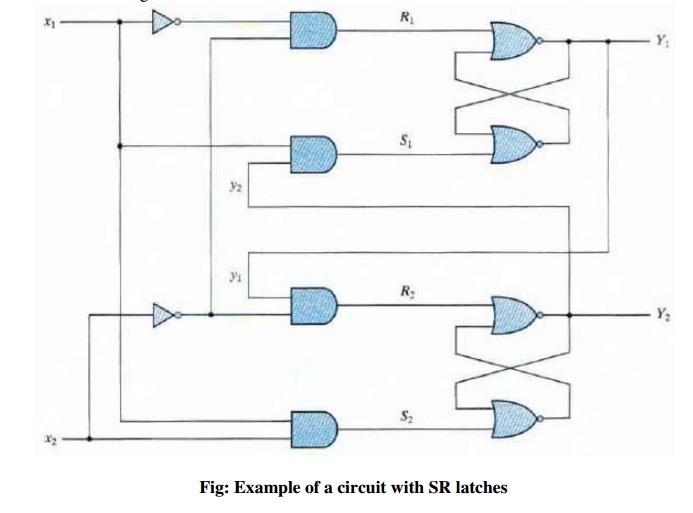
The first step is to obtain the Boolean functions for the S and R inputs in each latch:

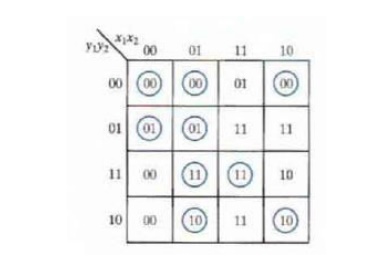
Investigation of the transition table reveals that the circuit is stable. There is a critical race condition when the circuit is initially in total state y1y2x1x2 = 1101 and x2 changes from 1 to 0. If Y1 changes to 0 before Y2, the circuit goes to total state 0100 instead of 0000.

SR Latch Excitation Table

Excitation table lists the required inputs S and R for each of the possible transitions from the secondary variable y to the excitation variable Y.

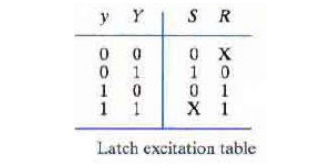
Useful for obtaining the Boolean functions for S and R and the circuit’s logic diagram from a give transition table.

Implementation Example

Consider the following transition table:

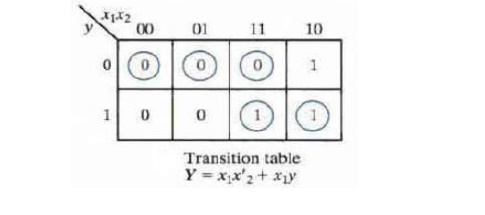
From the information given in the transition table and the SR latch excitation table, we can obtain maps for the S and R inputs of the latch:

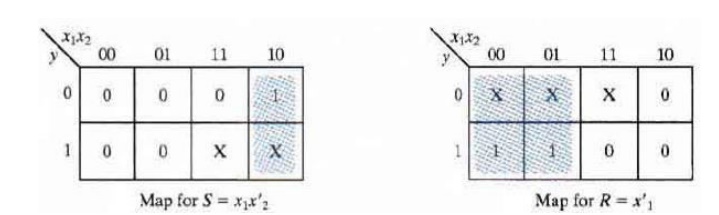
X represents a don’t care condition.

The maps are then used to derive the simplified Boolean functions:

The logic diagram consists of an SR latch and gates required to implement the S and R Boolean functions. The circuit when a NOR SR latch is used is as shown below:

With a NAND SR latch the complemented values for S and R must be used.