Race -Free State Assignment

RACE -FREE STATE ASSIGNMENT

Once a reduced flow table has been derived for an asynchronous sequential circuit, the next step in the design is to assign binary variables to each stable state. This assignment results in the transformation of the flow table into its equivalent transition table. The primary objective in choosing a proper binary state assignment is the prevention of critical races. Critical races can be avoided by making a binary state assignment in such a way that only one variable changes at any given time when a state transition occurs in the flow table.

ü Three-Row Flow-Table Example

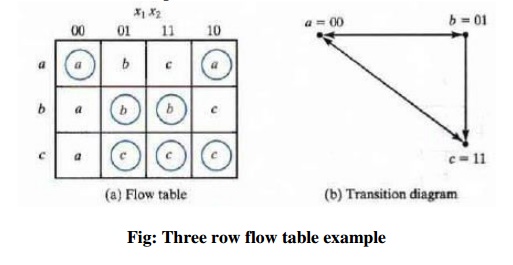
Fig: Three row flow table example

To avoid critical races, we must find a binary state assignment such that only one binary variable changes during each state transition. An attempt to find such an assignment is shown in the transition diagram. State a is assigned binary 00, and state c is assigned binary 11. This assignment will ca use a critical race during the transition from a to c because there are two changes in the binary state variables and the transition from a to c may occur directly or pass through b. Note that the transition from c to a also ca uses a race condition, but it is noncritical because the transition does not pass through other states.

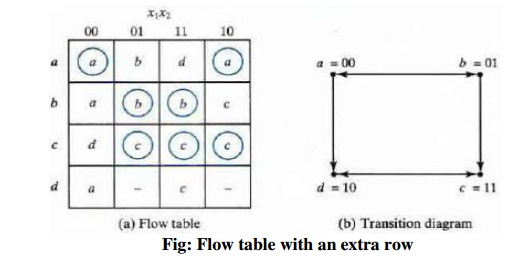
A race-free assignment can be obtained if we add an extra row to the flow table. The use of a fourth row does not increase the number of binary state variables, but it allows the formation of cycles between two stable states.

The transition table corresponding to the flow table with the indicated binary state assignment is shown in Fig. The two dashes in row d represent unspecified states that can be considered don't-care conditions. However, care must be taken not to assign 10 to these squares, in order to avoid the possibility of an unwanted stable state being established in the fourth row.

ü    Four-Row Flow-Table Example

A flow table with four rows requires a minimum of two state variables. Although a race-free assignment is sometimes possible with only two binary state variables, in many cases the requirement of extra rows to avoid critical races will dictate the use of three binary state variables

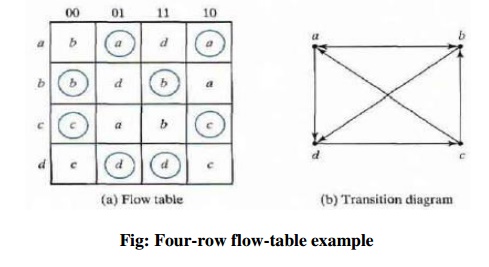
Fig: Four-row flow-table example

The following figure shows a state assignment map that is suitable for any four-row flow table. States a, b, c and d are the original states and e, f and g are extra states. The transition from a to d must be directed through the extra state e to produce a cycle so that only one binary variable changes at a time. Similarly, the transition from c to a is directed through g and the transition from d to c goes through f. By using the assignment given by the map, the four-row table can be expanded to a seven-row table that is free of critical races.

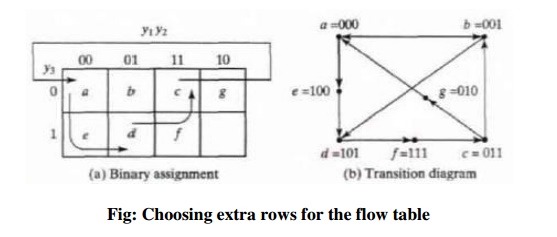
Fig: Choosing extra rows for the flow table

Note that although the flow table has seven rows there are only four stable states. The uncircled states in the three extra rows are there merely to provide a race-free transition between the stable states.

Fig: State assignment to modified flow table

ü    Multiple-Row Method

The method for making race-free stale assignments by adding extra rows in the flow table is referred to as the shared-row method. A second method called the multiple-row method is not as efficient, but is easier to apply. In multiple- row assignment each state in the original row table is replaced by two or more combinations of state variables.

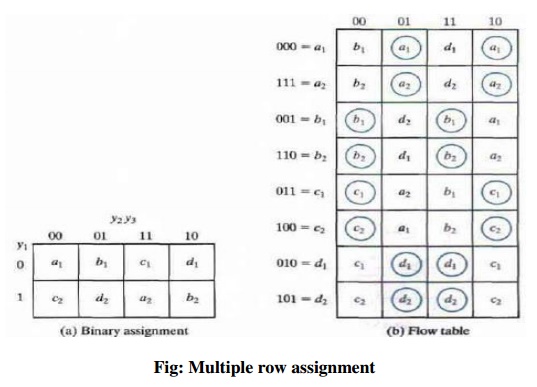
Fig: Multiple row assignment

There are two binary state variables for each stable state, each variable being the logical complement of the other. For example, the original state a is replaced with two equivalent states a₁ =000 and a₂ = 111. The output values, not shown here must be the same in a₁ and a₂. Note that a₁ is adjacent to b_1, c₂ and d₁, and a₂ is adjacent to c_1, b₂ and d₂, and similarly each state is adjacent to three states with different letter designations.

The expanded table is formed by replacing each row of the original table with two rows. In the multiple-row assignment, the change from one stable state 10 another will always cause a change of only one binary state variable. Each stable stale has two binary assignments with exactly the same output.