Rectangular or Uniform Distribution

Continuous distributions:

Rectangular or Uniform Distribution

Definition

 A random variable X is said to have a continuous Uniform distribution over the interval (a, b) if its probability density function is

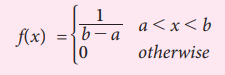
Characteristics of Uniform Distribution

i. a and b are the parameters of the Uniform distribution and we write X ~ U (a, b)

ii. The distribution is also known as Rectangular distribution, as the curve

iii. y = f(x) describes a rectangle over the x-axis and between ordinates at x = a and x= b.

(iv) f X ~ U (-a, a) then its p.d.f. is

Example 10.17

If X ~ U (200, 250) find its p.d.f and P (X > 230)

Solution:

Example 10.18

If X is a Uniform variate with the parameter 50 and100, find the mean, median and standard deviation.

Solution:

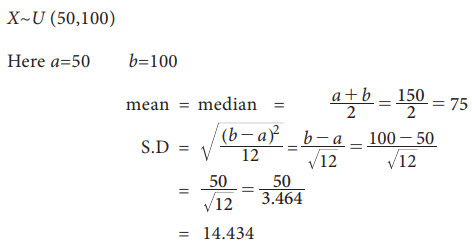
Example 10.19

If X is a random variable having a uniform distribution U (a,b) such that P(20<X<40)=0.2 and mean = 150, find a and b.

Solution:

(1)+(2) implies 2b = 400 and b = 200.

Substituting b in (2) we have a + 200 = 300 and that a =100.

a=100, b=200

X~U(100,200)

Example 10.20

If X is a Uniform variable U(a,b) with first and third quartiles 100 and 200, find the p.d.f of X.

Solution:

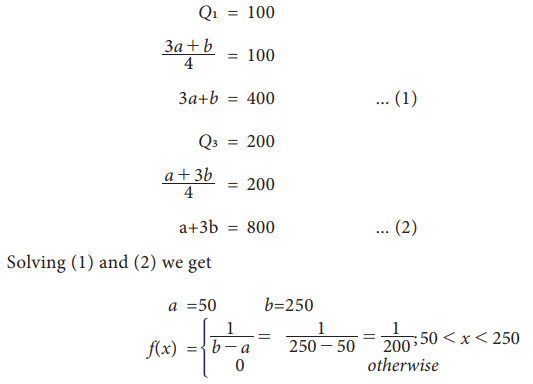
Example 10.21

Electric trains on a certain line run every 15 minutes between mid- night and six in the morning. What is the probability that a man entering the station at a random time during this period will have to wait at least ten minutes?

Let the random variable X denote the waiting time (in minutes).

The given assumption indicates that X is distributed Uniformly on (0,15).