Normal Distribution

NORMAL DISTRIBUTION

Introduction

 

The Normal distribution was first discovered by the English Mathematician De-Moivre in 1733, and he obtained this distribution as a limiting case of Binomial distribution and applied it to problems arising in the game of chance. In 1774 Laplace used it to estimate historical errors and in 1809 it was used by Gauss as the distribution of errors in Astronomy. Thus throughout the 18^th and 19^th centuries efforts were made for a common law for all continuous distributions which was then known as the Normal distribution.

 

Properties of Normal Distribution

 

Example 10.22

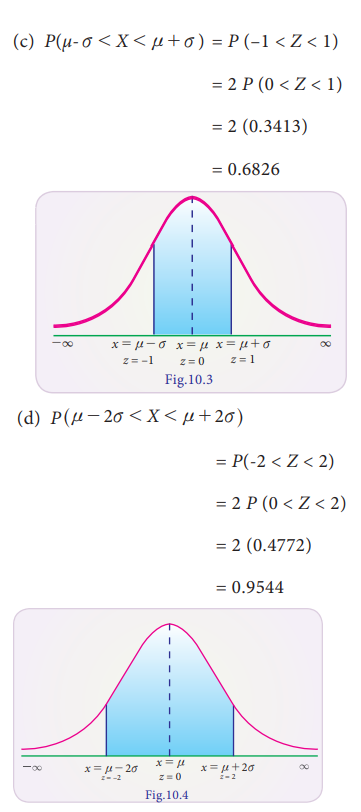
Find the area between z = 0 and z = 1.56

Solution:

P (0 < Z < 1.56) = 0.4406

(from the Normal Probability table)

 

Example 10.23

Find the area of the Standard Normal variate from – 1.96 to 0

Solution:

P (-1.96 < Z < 0)= P (0 < Z < 1.96) (by symmetry)

= 0.4750 (from the Normal Probability table)

 

Example 10.24

Find the area to the right of Z = 0.25

Solution:

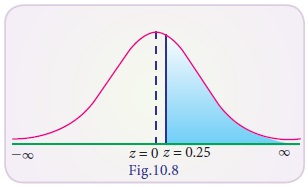
P (Z > 0.25) = P (0 < Z < ∞ ) – P (0 < Z < 0.25)

 = 0.5000 – 0.0987 (from table)

 = 0.4013

 

Example 10.25

Find the area to the left of Z = 1.5

Solution:

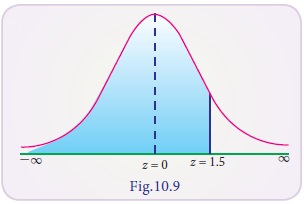
P (Z < 1.5) = P (- ∞< Z < 0) + P(0< Z < 1.5)

= 0.5000 + 0.4332 (from table)

= 0.9332

 

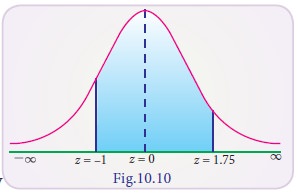
Example 10.26

Find the area between Z = -1 and Z = 1.75

Solution:

P(-1 < Z < 1.75)

P (-1 < Z < 0) + P (0 < Z < 1.75)

= P (0 < Z < 1) + P (0 < Z < 1.75)  by symmetry

= 0.3413 + 0.4599 = 0.8012

 

Example 10.27

Find the maximum value of the p.d.f of the Normal distribution with mean 40 and standard derivation 10. Also find its points of inflection.

Solution:

μ = 40

σ=10

Maximum value = f (x) 

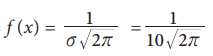
Points of inflection = μ±σ

= 40±10

= 30 and 50

 

Example 10.28

A Normal variable X has the mean 50 and the S.D 5. Find its mean deviation about mean and the quartile deviation.

Solution:

Given Mean =μ=50 , standard deviation σ = 5

Mean deviation above mean = 0.8 σ

= 0.8×5 = 4

Quartile deviation = 0.6745σ

= 0.6745×5

= 3.3725

 

Example 10.29

Find the quartiles of the Normal distribution having mean 60 and S.D 10.

Solution:

μ=60, σ=10

Let x₁ be the value such that the area from x₁ to μ is 25%

` P (x1<X < μ) = 25% = 0.25

 

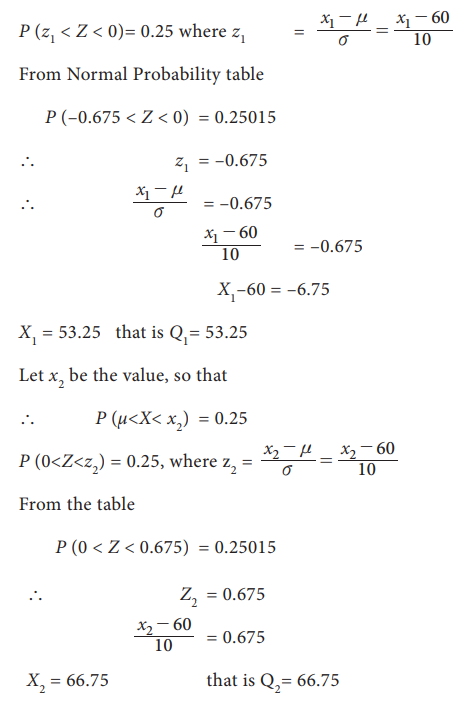
Example 10.30

The height of the rose plants in a garden is Normally distributed with a mean 100cms. Given that 10% of the plants have height greater than104cm. Find (i) The S.D of the distribution (ii) The number of plants have height greater than 105cms if there were 200 plants in the garden.

Solution:

The S.D of the distribution

Let X be the height of the rose plants that is Normally distributed.

Given: P (100 < x < 104) =40 %

P ( 0< Z <4/σ) = 0.40             ... (1)

But from table of area under Standard Normal curve

P ( 0< Z < 1.28 ) = 0.3997        ... (2)

 From (1) and (2)

4/ σ = 1.28

σ = 3.125

(ii) The number of plants with height greater than 105 cms if there were 200 plants in the garden.

X = 105

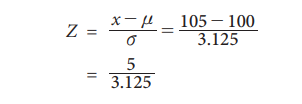
= 1.6

P(1.6 < Z < ∞) = 0.5-0.4452 = 0.0548

Number of plants = 200#0.0548 = 10.9600 ≈11

` 11 plants have height greater than 105cms.

 

Example 10.31

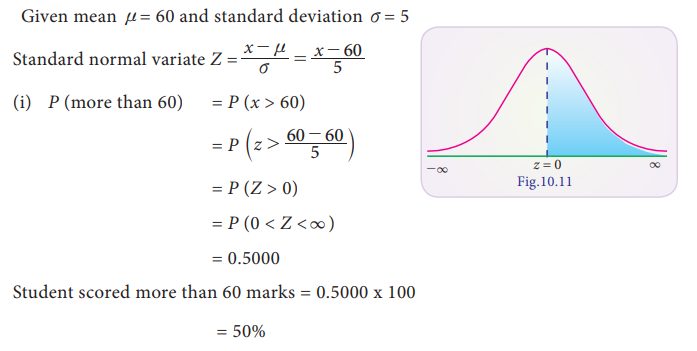
Students of a class were given an aptitude test. Their marks were found to be normally distributed with mean 60 and standard deviation 5. What percentage of students scored (i) more than 60 marks (ii) less than 56 marks (iii) between 45 and 65 marks.

Solution:

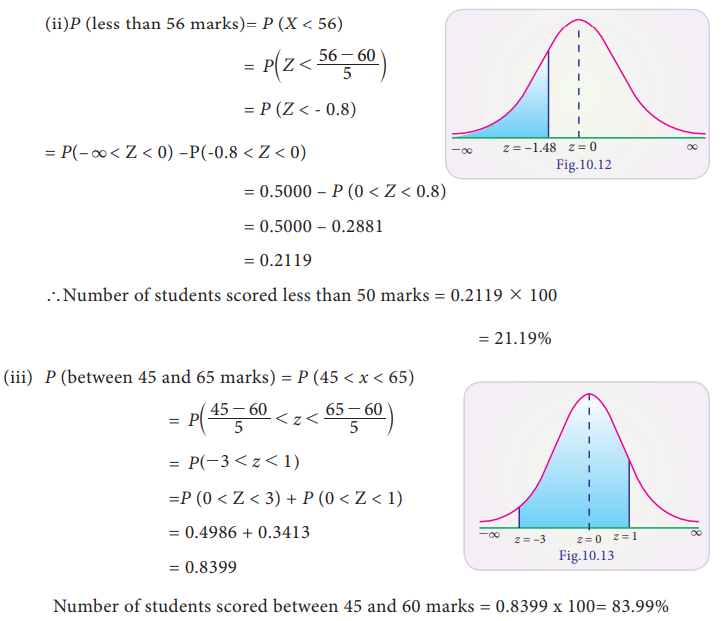
Number of students scored between 45 and 60 marks = 0.8399 x 100= 83.99%

 

Example 10.32

X has Normal distribution with mean 2 and standard deviation 3. Find the value of the variable x such that the probability of the interval from the mean to that value is 0.4115.

Solution:

 

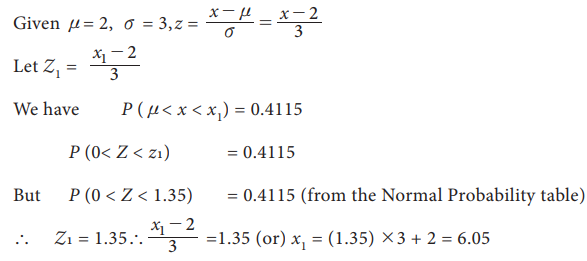
Example 10.33

In a Normal distribution 7% items are under 35 and 89% are under 63. Find its mean and standard deviation.

Solution: