Poission Distribution

POISSION DISTRIBUTION

Introduction

In a Binomial distribution with parameter n and p if the exact value of n is not definitely known and if p is very small then it is not possible to the find the binomial probabilities .Even if n is known and it is very large, calculations are tedious. In such situations a distribution called Poisson distribution is very much useful.

In 1837 French mathematician Simeon Dennis Poisson derived the distribution as a limiting case of Binomial distribution. It is called after his name as Poisson distribution.

Conditions:

i. The number of trails ‘n’ is indefinitely large i.e., n→ ∞

ii. The probability of a success ‘p’ for each trial is very small i.e.,p→ 0

iii. np= λ is finite

iv. Events are Independent

Definition

 A random variable X is said to follow a Poisson distribution if it assumes only non-negative integral values and its probability mass function is given by

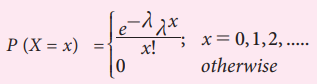
Characteristics of Poisson Distribution

(i) Poisson distribution is a discrete distribution i.e., X can take values 0, 1, 2,…

(ii) p is small, q is large and n is indefinitely large i.e., p →0 q →1 and n→3 and np is finite

(iii) Values of constants : (a) Mean = λ = variance (b) Standard deviation = √λ (c) Skewness = 1/ √λ (iv) Kurtosis =1/ λ

(iv) It may have one or two modes

(v) If X and Y are two independent Poisson variates, X+Y is also a Poisson variate.

(vi) If X and Y are two independent Poisson variates, X-Y need not be a Poisson variate.

(vii) Poisson distribution is positively skewed.

(viii) It is leptokurtic.

Some examples:

i.               The event of a student getting first mark in all subjects and at all the examinations

ii.               The event of finding a defective item from the production of a reputed company

iii.               The number of blinds born in a particular year

iv.               The number of mistakes committed in a typed page

v.               The number of traffic accidents per day at a busy junction.

vi.               The number of death claims received per day by an insurance company.

Example 10.11

If 2% of electric bulbs manufactured by a certain company are defective find the probability that in a sample of 200 bulbs (i) less than 2 bulbs are defective (ii) more than 3 bulbs are defective. [e-4 = 0.0183]

Solution:

Let X denote the number of defective bulbs

Example 10.12

In a Poisson distribution 3P(X= 2) = P(X = 4). Find its parameter 'λ

Solution:

Example 10.13

Find the skewness and kurtosis of a Poisson variate with parameter 4.

Solution:

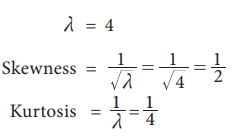
Example 10.14

If there are 400 errors in a book of 1000 pages, find the probability that a randomly chosen page from the book has exactly 3 errors.

Solution:

Let X denote the number of errors in pages

Example 10.15

If X is a Poisson variate with P(X=0) = 0.2725, find P(X=1)

Solution:

Example 10.16

The probability of safety pin manufactured by a firm to be defective is 0.04. (i) Find the probability that a box containing 100 such pins has one defective pin . (ii) Among 200 such boxes, how many boxes will have no defective pin

Solution:

Let X denote the number boxes with defective pins