Binomial Distribution

BINOMIAL DISTRIBUTION

Introduction

Binomial distribution was discovered by James Bernoulli (1654 – 1705) in the year 1700 and was first published in 1713 eight years after his death. The distribution of the Sum of n independent Bernoulli variables is known as a Binomial distribution.

That is the sum of outcome of n independent experiments of Bernoulli trials, in each of which the probability of success is constant p and the probability of failure is q=1– p is called Binomial experiment.

Conditions for Binomial Distribution

We get the Binomial Distribution under the following experimental conditions:

i.               The number of trials `n’ is finite

ii.               The trials are independent of each other

iii.               The probability of success `p’ is same for each trial

iv.               Each trial must result in a success or a failure.

Characteristics of Binomial Distribution

i. Binomial distribution is a discrete distribution i.e., X can take values 0, 1, 2, ... n where `n’ is finite .

ii. Constants of the distributions are:

Mean = np; Variance = npq; Standard deviation = √npq

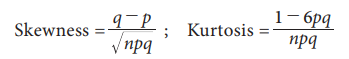
iii. It may have one or two modes.

iv. If X~B( n₁,p) and Y~B(n₂,p) and that X and Y are independent then X+Y~B(n₁+n₂,p)

v. If `n’ independent trials are repeated N times the expected frequency of `x’ successes is N× nC_x p^x q^n–x

vi. If p = 0.5, the distribution is symmetric.

Example 10.1

Comment on the following 'The mean of binomial distribution is 5 and its variance is 9'.

Solution:

Given mean np = 5 and variance npq = 9

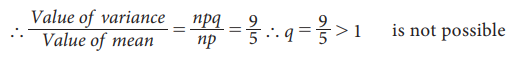
as 0 < q < 1 and hence the given statement is wrong.

Example 10.2

Eight coins are tossed simultaneously. Find the probability of getting atleast six heads.

Solution:

Example 10.3

Ten coins are tossed simultaneously. Find the probability of getting (i) atleast seven heads (ii) exactly seven heads (iii) atmost seven heads.

Solution:

X denote the number of heads appear

Example 10.4

With usual notation find p for Binomial random variable X if n = 6 and 9 P(x = 4) = P (x = 2)

Solution:

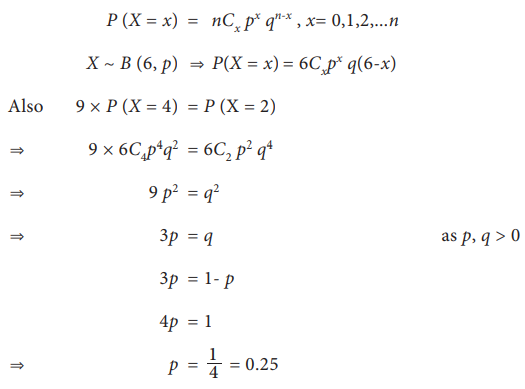
Example 10.5

A Binomial distribution has parameters n=5 and p=1/4. Find the Skewness and Kurtosis.

Solution:

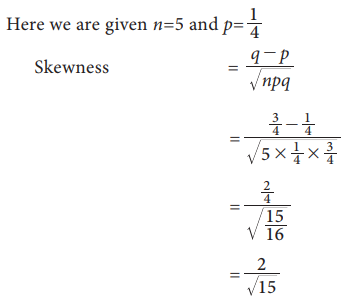
Finding: The distribution is positively skewed.

Kurtosis

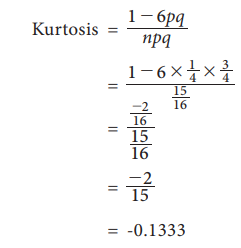
Finding: The distribution is Platykurtic.

Example 10.6

In a Binomial distribution with 7 trials, P(X=3)=P(X=4) Check whether it is a symmetrical distribution?

Solution:

Hence the given Binomial distribution is symmetrical.

Example 10.7

From a pack of 52 cards 4 cards are drawn one after another with replacement. Find the mean and variance of the distribution of the number of kings.

Solution:

Success X=event of getting king in a draw

p=probability of getting king in a single trial

Example 10.8

In a street of 200 families, 40 families purchase the Hindu newspaper. Among the families a sample of 10 families is selected, find the probability that

i. Only one family purchase the news paper

ii. No family purchasing

iii. Not more than one family purchase it

Solution:

X ~ B (n, p)

 P (X = x) = nC_xp^x q^n-x , x= 0,1,2,...n

Let X denote the number of families purchasing Hindu Paper

p = Probability of their family purchasing the Hindu

(i) Only one family purchase the Hindu

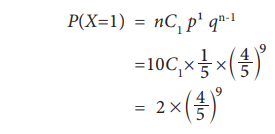
(ii) No family purchasing the Hindu

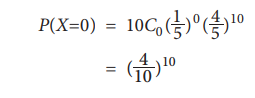
(iii) Not more than one family purchasing The Hindu means that X≤1

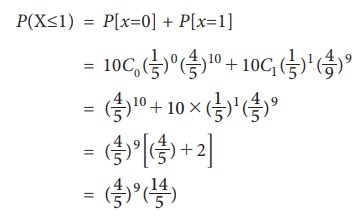
Example 10.9

In a tourist spot, 80% of tourists are repeated visitors. Find the distribution of the numbers of repeated visitors among 4 selected peoples visiting the place. Also find its mode or the maximum visits by a visitor.

Solution:

Let the random variable X denote the number of repeated visitors.

X ~ B (n, p)

 P (X = x) = nC_xp^xq^n-x , x= 0,1,2,...n

 It is a Binomial Distribution with n=4

Example 10.10

In a college, 60% of the students are boys. A sample of 4 students of the college, is taken, find the minimum number of boys should it have so that probability up to that number is ≥ 1/2.

Solution:

It is given that 60% of the students of the college are boys and the selection probability for a boy is 60% or 0.6 As we are taking four samples, the number of trials n = 4. The selection process is independent.

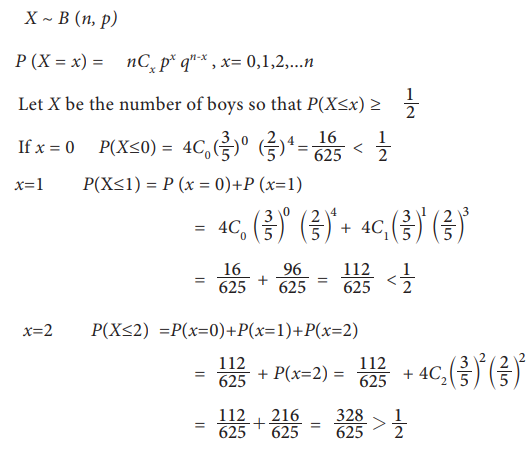
Therefore the sample should contain a minimum of 2 boys.