Railway Engineering: Turnouts

Turnouts

The simplest arrangement of points and crossing can be found on a turnout taking off from a straight track. There are two standard methods prevalent for designing a turnout. These are the (a) Coles method and the (b) IRS method.

These methods are described in detail in the following sections.

The important terms used in describing the design of turnouts are defined as follows.

Curve lead (CL) This is the distance from the tangent point (T) to the theoretical nose of crossing (TNC) measured along the length of the main track.

Switch lead (SL) This is the distance from the tangent point (T) to the heel of the switch (TL) measured along the length of the main track.

Lead of crossing (L) This is the distance measured along the length of the main track as follows:

Lead of crossing (L) = curve lead (CL) - switch lead (SL)

Gauge (G) This is the gauge of the track.

Heel divergence (D) This is the distance between the main line and the turnout side at the heel.

Angle of crossing ( a )  This is the angle between the main line and the tangent of

the turnout line.

Radius of turnout (R) This is the radius of the turnout. It may be clarified that the radius of the turnout is equal to the radius of the centre line of the turnout (R₁) plus half the gauge width.

R = R₁ + 0.5G

As the radius of a curve is quite large, for practical purposes, R may be taken to be equal to R₁.

Special fittings with turnouts

Some of the special fittings required for use with turnouts are enumerated below.

Distance blocks Special types of distance blocks with fishing fit surfaces are provided at the nose of the crossing to prevent any vertical movement between the wing rail and the nose of the crossing.

Flat bearing plates As turnouts do not have any cant, flat bearing plates are provided under the sleepers.

Spherical washers These are special types of washers and consist of two pieces with a spherical point of contact between them. This permits the two surfaces to lie at any angle to each other. These washers are used for connecting two surfaces that are not parallel to one another. Normally, tapered washers are necessary for connecting such surfaces. Spherical washers can adjust to the uneven bearings of the head or nut of a bolt and so are used on all bolts in the heel and the distance blocks behind the heel on the left-hand side of the track.

Slide chairs These are provided under tongue rails to allow them to move laterally. These are different for ordinary switches and overriding switches.

Grade off chairs These are special chairs provided behind the heel of the switches to give a suitable ramp to the tongue rail, which is raised by 6 mm at the heel.

Gauge tie plates These are provided over the sleepers directly under the toe of the switches, and under the nose of the crossing to ensure proper gauge at these locations.

Stretcher bars These are provided to maintain the two tongue rails at an exact distance.

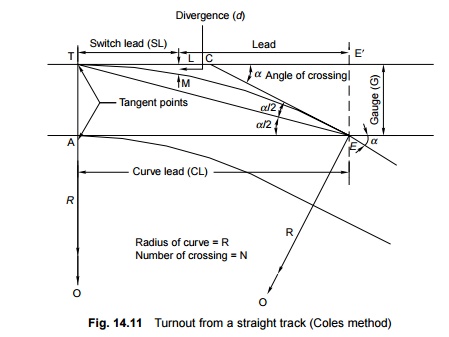
Coles method

This is a method used for designing a turnout taking off from a straight track (Fig. 14.11). The curvature begins from a point on the straight main track ahead of the toe of the switch at the theoretical toe of switch (TTS) and ends at the theoretical nose of crossing (TNC). The heel of the switch is located at the point where the offset of the curve is equal to the heel divergence. Theoretically, there would be no kinks in this layout, had the tongue rail been curved as also the wing rail up to the TNC. Since tongue rails and wing rails are not curved generally, there are the following three kinks in this layout.

(a) The first kink is formed at the actual toe of the switch.

(b) The second kink is formed at the heel of the switch.

(c)  The third kink is formed at the first distance block of the crossing. The notations used in Fig. 14.11 are the following.

Curve lead (CL) = AE = TE'

Switch lead (SL) = TL

Lead of crossing (L) = LE'

Gauge of track (G) = AT = EE'

Angle of the crossing (a ) = ÐCEA = ÐECE¢

Heel of divergence (d) = LM

Number of the crossing (N) = cota

Radius of outer rail of turnout curve (R) = OE = OT (O is the centre of the turnout curve)

Calculations

Curve lead (CL) In DATE ,

= 2GN (approximately)

Switch lead (SL) TL is the length of the tangent with an offset LM = D = heel divergence.

From the properties of triangles, SL × SL = d (2R - d)

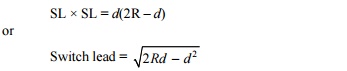
Lead of crossing (L)

L = curve lead - switch lead

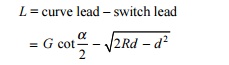
Radius of curve (R)  In DAOE ,

OE = OT = R, OA = R -  G

OE² = OA² + AE²

OE² = (R - G) ² + (curve lead)²

Example 14.1 Calculate the lead and radius of a 1 in 8.5 BG turnout for 90 R rails using Coles method.

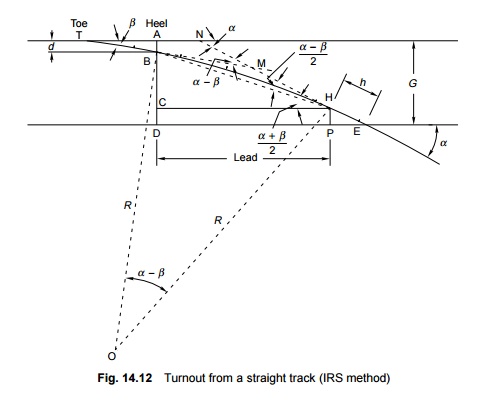
IRS method

In this layout (Fig. 14.12), the curve begins from the heel of the switch and ends at the toe of the crossing, which is at the centre of the first distance block. The crossing is straight and no kink is experienced at this point. The only kink occurs at the toe of the switch. This is the standard layout used on Indian Railways. The calculations involved in this method are somewhat complicated and hence this method is used only when precision is required.

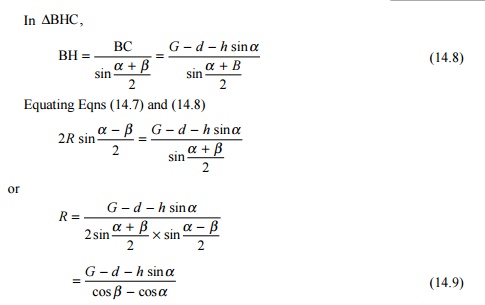
Example 14.2 Calculate the lead and radius of a 1 in 8.5 BG turnout with straight switches. Use the IRS method.

Example 14.3 A turnout is to be laid off a straight BG track with a 1 in 12 crossing. Determine the lead and radius of the turnout with the help of the following data: heel divergence (d) = 133 mm, crossing angle (a ) = 4 o 45 ' 49'', switch angle ( b ) = 1 o 8 ' 00'', straight length between the theoretical nose of crossing and the tangent point of crossing (h) = 1.418 m.

Standard turnouts and permissible speeds

On Indian Railways, normally 1 in 8.5 turnouts are used for goods trains while 1 in 12 and 1 in 16 turnouts are used for passenger trains. Recently 1 in 20 and 1 in 24 turnouts have also been designed by the RDSO, to be used to permit higher speeds for fast trains on the turnout side. The maximum speeds permitted on these turnouts are given in Table 14.5.

Table 14.5   Permissible speeds on turnouts

Source: Indian Railway Permanent Way Manual (IRPWM)-Correction slip no. 94 dated 1 June 2004.

* As per the Indian Railway way and works (IRWW) manual, a speed of 15 km/h was originally permitted on 1 in 8.5 turnouts. However, due to a subsequent number of derailments of passenger trains on turn-in curves, the speeds on these turnouts have row been reduced to 10 km/h only.

^†  The figures in the second row correspond to curved switches.

^‡ A speed of 30 km/h is also permitted on 1 in 12 turnouts on those interlocked sections where all turnouts over which a running train may pass are 1 in 12 throughout the section and the locomotives are fitted with speedometers. In all other cases, speed is restricted to 15 km/h only.

^¶  60 km/h permitted only for high-speed turnouts to Drg. No. RDST/T-403.

Turnout with Curved Switches

The following formulae are used for the calculation of turnouts with curved switches

where R is the radius of the outer lead rail, G is the gauge, h is the lead of the straight leg of the crossing ahead of TNC up to the TP of the lead curve, t is the thickness of the switch at the toe, I is the distance from the toe of the switch to the point where the tangent drawn to the extended lead curve is parallel to the main line gauge face, V is the distance between the main line gauge face and the tangent drawn to the lead curve from a distance l from the toe, y is the vertical ordinate along the Y-axis, a is the crossing angle, and b is the switch angle.

Layout of Turnout

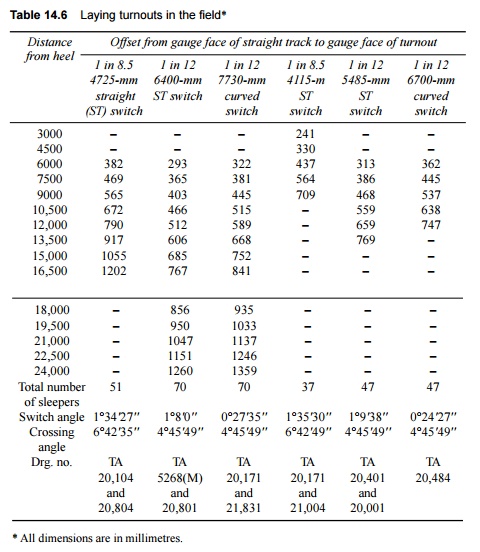
To lay out a turnout in the field, the values of offsets from the gauge face of the straight track to the gauge face of the turnout may be adopted from Table 14.6.

Table 14.6   Laying turnouts in the field*