Chapter: Introduction to the Design and Analysis of Algorithms : Transform and Conquer
Problem Reduction
Problem Reduction
Here is my version of a well-known joke about
mathematicians. Professor X, a noted mathematician, noticed that when his wife
wanted to boil water for their tea, she took their kettle from their cupboard,
filled it with water, and put it on the stove. Once, when his wife was away (if
you have to know, she was signing her best-seller in a local bookstore), the
professor had to boil water by himself. He saw that the kettle was sitting on
the kitchen counter. What did Professor X do? He put the kettle in the cupboard
first and then proceeded to follow his wifeŌĆÖs routine.

The way Professor X approached his task is an
example of an important problem-solving strategy called problem reduction. If you
need to solve a problem, reduce it to another problem that you know how to
solve (Figure 6.15).
The joke about the professor notwithstanding,
the idea of problem reduction plays a central role in theoretical computer
science, where it is used to classify problems according to their complexity.
We will touch on this classification in Chapter 11. But the strategy can be
used for actual problem solving, too. The practical difficulty in applying it
lies, of course, in finding a problem to which the problem at hand should be
reduced. Moreover, if we want our efforts to be of practical value, we need our
reduction-based algorithm to be more efficient than solving the original
problem directly.
Note that we have already encountered this
technique earlier in the book. In Section 6.5, for example, we mentioned the
so-called synthetic division done by applying HornerŌĆÖs rule for polynomial
evaluation. In Section 5.5, we used the following fact from analytical
geometry: if p1(x1, y1), p2(x2, y2), and p3(x3, y3) are three arbitrary points in the plane, then
the determinant
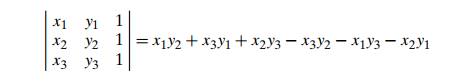
is positive if and only if the point p3 is to
the left of the directed line p1p2 through points p1 and p2. In other words, we reduced a geometric question about the
relative locations of three points to a question about the sign of a
determinant. In fact, the entire idea of analytical geometry is based on
reducing geometric problems to algebraic ones. And the vast majority of
geometric algorithms take advantage of this historic insight by Rene┬┤ Descartes
(1596ŌĆō1650). In this section, we give a few more examples of algorithms based
on the strategy of problem reduction.
Computing the Least Common
Multiple
Recall that the least common multiple of
two positive integers m and n, denoted lcm(m, n), is defined as the smallest integer that is
divisible by both m and n. For example, lcm(24, 60) = 120, and lcm(11, 5) = 55. The least common multiple is one of the
most important notions in elementary arithmetic and algebra. Perhaps you
remember the following middle-school method for computing it: Given the prime
factorizations of m and n, compute the product of all the common prime
factors of m and n, all the prime factors of m that are not in n, and all the prime factors of n that are not in m. For example,

lcm(24, 60) = (2 . 2 . 3) . 2 . 5 = 120.
As a computational procedure, this algorithm
has the same drawbacks as the middle-school algorithm for computing the
greatest common divisor discussed in Section 1.1: it is inefficient and
requires a list of consecutive primes.
A much more efficient algorithm for computing
the least common multiple can be devised by using problem reduction. After all,
there is a very efficient algorithm (EuclidŌĆÖs algorithm) for finding the
greatest common divisor, which is a product of all the common prime factors of m and n. Can we find a formula relating lcm(m, n) and gcd(m, n)? It is not difficult to see that the product
of lcm(m, n) and gcd(m, n) includes every factor of m and n exactly once and hence is simply equal to the
product of m and n. This observation leads to the formula

where gcd(m, n) can be computed very efficiently by EuclidŌĆÖs
algorithm.
Counting Paths in a Graph
As our next example, we consider the problem of
counting paths between two vertices in a graph. It is not difficult to prove by
mathematical induction that the number of different paths of length k > 0 from the ith vertex to the j th vertex of a graph (undirected or directed)
equals the (i, j )th element of Ak where A is the adjacency matrix of the graph.
Therefore, the problem of counting a graphŌĆÖs paths can be solved with an
algorithm for computing an appropriate power of its adjacency matrix. Note that
the exponentiation algorithms we discussed before for computing powers of
numbers are applicable to matrices as well.
As a specific example, consider the graph of
Figure 6.16. Its adjacency matrix A and its square A2 indicate the numbers of paths of length 1 and
2, respectively, between the corresponding vertices of the
graph. In particular, there are three

paths of length 2 that start and end at vertex a (a ŌłÆ b ŌłÆ a, a ŌłÆ c ŌłÆ a, and a ŌłÆ d ŌłÆ a); but there is only one path of length 2 from a to c (a ŌłÆ d ŌłÆ c).
Reduction of Optimization
Problems
Our next example deals with solving
optimization problems. If a problem asks to find a maximum of some function, it
is said to be a maximization problem; if it asks to find a functionŌĆÖs minimum,
it is called a minimization problem. Suppose now that you need to find a
minimum of some function f (x) and you have an algorithm for function
maximization. How can you take advantage of the latter? The answer lies in the
simple formula
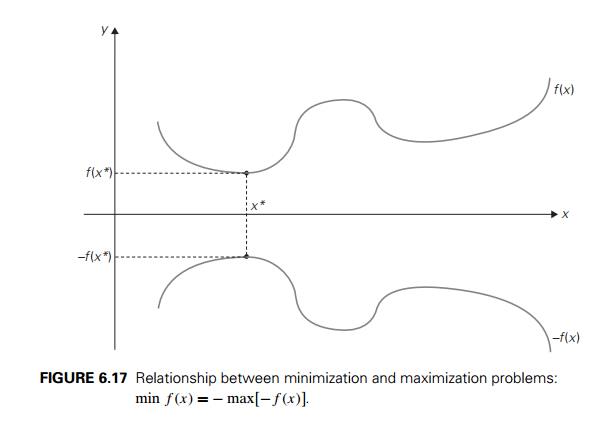
min f (x) = ŌłÆ max[ŌłÆf (x)].
In other words, to minimize a function, we can maximize
its negative instead and, to get a correct minimal value of the function
itself, change the sign of the answer. This property is illustrated for a
function of one real variable in Figure 6.17.
Of course, the formula
max f (x) = ŌłÆ min[ŌłÆf (x)]
is valid as well; it shows how a maximization
problem can be reduced to an equivalent minimization problem.
This relationship between minimization and
maximization problems is very general: it holds for functions defined on any
domain D. In particular, we can
apply it to functions of several variables
subject to additional constraints. A very important class of such problems is
introduced below in this section.
Now that we are on the topic of function
optimization, it is worth pointing out that the standard calculus procedure for
finding extremum points of a function is, in fact, also based on problem
reduction. Indeed, it suggests finding the functionŌĆÖs derivative f (x) and then solving the equation f (x) = 0 to find the functionŌĆÖs critical points. In
other words, the optimization problem is reduced to the problem of solving an
equation as the principal part of finding extremum points. Note that we are not
calling the calculus procedure an algorithm, since it is not clearly defined. In
fact, there is no general method for solving equations. A little secret of
calculus textbooks is that problems are carefully selected so that critical
points can always be found without difficulty. This makes the lives of both
students and instructors easier but, in the process, may unintentionally create
a wrong impression in studentsŌĆÖ minds.
Linear Programming
Many problems of optimal decision making can be
reduced to an instance of the linear programming problemŌĆöa problem
of optimizing a linear function of several variables subject to constraints in
the form of linear equations and linear inequalities.
EXAMPLE 1 Consider a university endowment that needs to
invest $100 million. This sum has to be split between three types of investments:
stocks, bonds, and cash. The endowment managers expect an annual return of 10%,
7%, and 3% for their stock, bond, and cash investments, respectively. Since
stocks are more risky than bonds, the endowment rules require the amount
invested in stocks to be no more than one-third of the moneys invested in
bonds. In addition, at least 25% of the total amount invested in stocks and
bonds must be invested in cash. How should the managers invest the money to
maximize the return?
Let us create a mathematical model of this
problem. Let x, y, and z be the amounts (in millions of dollars)
invested in stocks, bonds, and cash, respectively. By using these variables, we
can pose the following optimization problem:
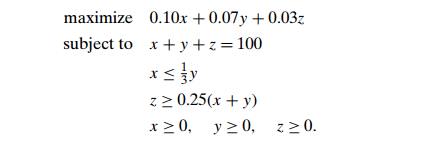
Although this example is both small and simple,
it does show how a problem of optimal decision making can be reduced to an
instance of the general linear programming problem
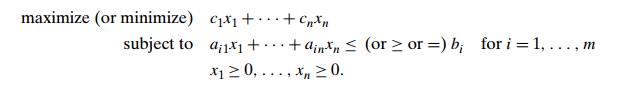
(The last group of constraintsŌĆöcalled the
nonnegativity constraintsŌĆöare, strictly speaking, unnecessary because they are
special cases of more general constraints ai1x1 + . . . + ainxn
Ōēź bi, but it is convenient to treat them separately.)
Linear programming has proved to be flexible
enough to model a wide variety of important applications, such as airline crew
scheduling, transportation and communication network planning, oil exploration
and refining, and industrial production optimization. In fact, linear
programming is considered by many as one of the most important achievements in
the history of applied mathematics.
The classic algorithm for this problem is
called the simplex method (Sec-tion 10.1). It was discovered by the U.S.
mathematician George Dantzig in the 1940s [Dan63]. Although the worst-case
efficiency of this algorithm is known to be exponential, it performs very well
on typical inputs. Moreover, a more recent al-gorithm by Narendra Karmarkar
[Kar84] not only has a proven polynomial worst-case efficiency but has also
performed competitively with the simplex method in empirical tests.
It is important to stress, however, that the
simplex method and KarmarkarŌĆÖs algorithm can successfully handle only linear
programming problems that do not limit its variables to integer values. When
variables of a linear programming problem are required to be integers, the
linear programming problem is said to be an integer linear programming
problem. Except for some special cases (e.g., the assignment problem and the
problems discussed in Sections 10.2ŌĆō10.4), integer linear programming problems
are much more difficult. There is no known polynomial-time algorithm for
solving an arbitrary instance of the general integer linear programming problem
and, as we see in Chapter 11, such an algorithm quite possibly does not exist. Other
approaches such as the branch-and-bound technique discussed in Section 12.2 are
typically used for solving integer linear programming problems.
EXAMPLE 2 Let us see how the knapsack problem can be
reduced to a linear programming problem. Recall from Section 3.4 that the knapsack
problem can be posed as follows. Given a knapsack of capacity W and n items of weights w1, . . .
, wn and
values v1, . . . , vn, find the most valuable subset of the items
that fits into the knapsack. We consider first the continuous (or fractional)
version of the problem, in which any fraction of any item given can be taken
into the knapsack. Let xj , j = 1, . . . , n, be a variable representing a fraction of item
j taken into the knapsack. Obviously, xj must satisfy the inequality 0 Ōēż xj Ōēż 1. Then the total
EXAMPLE 2 Let us see how the knapsack problem
can be reduced to a linear programming problem. Recall from Section 3.4 that
the knapsack problem can be posed as follows. Given a knapsack of capacity W
and n items of weights w1, . . . , wn and values v1, . . . , vn, find the most
valuable subset of the items that fits into the knapsack. We consider first the
continuous (or fractional) version of the problem, in which any fraction of any
item given can be taken into the knapsack. Let xj , j = 1, . . . , n, be a
variable representing a fraction of item j taken into the knapsack. Obviously,
xj must satisfy the inequality 0 Ōēż xj Ōēż 1. Then the total


This seemingly minor modification makes a
drastic difference for the com-plexity of this and similar problems constrained
to take only discrete values in their potential ranges. Despite the fact that
the 0-1 version might seem to be eas-ier because it can ignore any subset of
the continuous version that has a fractional value of an item, the 0-1 version
is, in fact, much more complicated than its con-tinuous counterpart. The reader
interested in specific algorithms for solving this problem will find a wealth
of literature on the subject, including the monographs [Mar90] and [Kel04].
Reduction to Graph Problems
As we pointed out in Section 1.3, many problems
can be solved by a reduction to one of the standard graph problems. This is
true, in particular, for a variety of puzzles and games. In these applications,
vertices of a graph typically represent possible states of the problem in
question, and edges indicate permitted transi-tions among such states. One of
the graphŌĆÖs vertices represents an initial state and another represents a goal
state of the problem. (There might be several vertices of the latter kind.)
Such a graph is called a state-space graph. Thus, the
transfor-mation just described reduces the problem to the question about a path
from the initial-state vertex to a goal-state vertex.

EXAMPLE Let us revisit the classic river-crossing
puzzle that was included in the exercises for Section 1.2. A peasant finds himself on a river
bank with a wolf, a goat, and a head of cabbage. He needs to transport all
three to the other side of the river in his boat. However, the boat has room
only for the peasant himself and one other item (either the wolf, the goat, or
the cabbage). In his absence, the wolf would eat the goat, and the goat would
eat the cabbage. Find a way for the peasant to solve his problem or prove that
it has no solution.
The state-space graph for this problem is given
in Figure 6.18. Its vertices are labeled to indicate the states they represent:
P, w, g, c stand for the peasant, the wolf, the goat, and the cabbage,
respectively; the two bars | | denote the river; for convenience, we also
label the edges by indicating the boatŌĆÖs occupants for each crossing. In terms
of this graph, we are interested in finding a path from the initial-state
vertex labeled Pwgc| | to the final-state vertex labeled | |Pwgc.
It is easy to see that there exist two distinct
simple paths from the initial-state vertex to the final state vertex (what are
they?). If we find them by applying breadth-first search, we get a formal proof
that these paths have the smallest number of edges possible. Hence, this puzzle
has two solutions requiring seven river crossings, which is the minimum number
of crossings needed.
Our success in solving this simple puzzle
should not lead you to believe that generating and investigating state-space
graphs is always a straightforward task. To get a better appreciation of them,
consult books on artificial intelligence (AI), the branch of computer science
in which state-space graphs are a principal subject.
In this book, we deal with an important special
case of state-space graphs in Sections 12.1 and 12.2.
Exercises 6.6
1.
a. Prove the equality
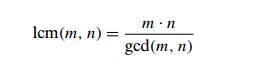
that underlies the algorithm for computing lcm(m, n).
EuclidŌĆÖs
algorithm is known to be in O(log n). If it is the algorithm that is used for
computing gcd(m, n), what is the efficiency of the algorithm for computing lcm(m, n)?
You are
given a list of numbers for which you need to construct a min-heap. (A min-heap
is a complete binary tree in which every key is less than or equal to the keys
in its children.) How would you use an algorithm for constructing a max-heap (a
heap as defined in Section 6.4) to construct a min-heap?
Prove
that the number of different paths of length k > 0 from the ith vertex to the j th vertex in a graph (undirected or directed)
equals the (i, j )th element of Ak where A is the adjacency matrix of the graph.
a. Design an algorithm with a time efficiency better than cubic for
checking whether a graph with n vertices contains a cycle of length 3 [Man89].
Consider
the following algorithm for the same problem. Starting at an arbi-trary vertex,
traverse the graph by depth-first search and check whether its depth-first
search forest has a vertex with a back edge leading to its grand-parent. If it
does, the graph contains a triangle; if it does not, the graph does not contain
a triangle as its subgraph. Is this algorithm correct?
Given n > 3 points P1 = (x1, y1), . . .
, Pn = (xn, yn) in the coordinate plane, design an algorithm
to check whether all the points lie within a triangle with its vertices at
three of the points given. (You can either design an algorithm from scratch or
reduce the problem to another one with a known algorithm.)
Consider
the problem of finding, for a given positive integer n, the pair of integers whose sum is n and whose product is as large as possible.
Design an efficient algorithm for this problem and indicate its efficiency
class.
7. The assignment problem introduced in Section
3.4 can be stated as follows: There are n people who need to be assigned to execute n jobs, one person per job. (That is, each person is assigned to
exactly one job and each job is assigned to exactly one person.) The cost that
would accrue if the ith person is assigned to the j th job is a known quantity C[i, j ] for each pair i, j = 1, . . . , n. The problem is to assign the people to the
jobs to minimize the total cost of the assignment. Express the assignment
problem as a 0-1 linear programming problem.
8. Solve the instance of the linear programming
problem given in Section 6.6:

9. The graph-coloring problem is usually stated as the vertex-coloring prob-lem: Assign the smallest number of colors to vertices of a given graph so that no two adjacent vertices are the same color. Consider the edge-coloring problem: Assign the smallest number of colors possible to edges of a given graph so that no two edges with the same endpoint are the same color. Ex-plain how the edge-coloring problem can be reduced to a vertex-coloring problem.

11. Jealous husbands There are n Ōēź 2 married couples who need to cross a river. They have a boat that can hold no more than two people at a time. To complicate matters, all the husbands are jealous and will not agree on any crossing procedure that would put a wife on the same bank of the river with another womanŌĆÖs husband without the wifeŌĆÖs husband being there too, even if there are other people on the same bank. Can they cross the river under such constraints?
Solve
the problem for n = 2.
Solve
the problem for n = 3, which is the classical version of this
problem.
Does the
problem have a solution for n Ōēź 4? If it does, indicate how many river
crossings it will take; if it does not, explain why.
12. Double-n
dominoes Dominoes are small
rectangular tiles with dots called spots
or pips embossed at both halves of the tiles. A standard ŌĆ£double-sixŌĆØ domino
set has 28 tiles: one for each unordered pair of integers from (0, 0) to (6, 6). In general, a ŌĆ£double-nŌĆØ domino set would consist of domino tiles for each unordered pair
of integers from (0, 0) to (n, n). Determine all values of n for which one constructs a ring made up of all the tiles in a
double-n domino set.
Related Topics