Presorting

Presorting

Presorting is an old idea in computer science. In fact, interest in sorting algorithms is due, to a significant degree, to the fact that many questions about a list are easier to answer if the list is sorted. Obviously, the time efficiency of algorithms that involve sorting may depend on the efficiency of the sorting algorithm being used. For the sake of simplicity, we assume throughout this section that lists are implemented as arrays, because some sorting algorithms are easier to implement for the array representation.

So far, we have discussed three elementary sorting algorithms—selection sort, bubble sort, and insertion sort—that are quadratic in the worst and average cases, and two advanced algorithms—mergesort, which is always in  (n log n), and quicksort, whose efficiency is also  (n log n) in the average case but is quadratic in the worst case. Are there faster sorting algorithms? As we have already stated in Section 1.3 (see also Section 11.2), no general comparison-based sorting algorithm can have a better efficiency than n log n in the worst case, and the same result holds for the average-case efficiency.¹

Following are three examples that illustrate the idea of presorting. More examples can be found in this section’s exercises.

EXAMPLE 1 Checking element uniqueness in an array If this element unique-ness problem looks familiar to you, it should; we considered a brute-force algo-rithm for the problem in Section 2.3 (see Example 2). The brute-force algorithm compared pairs of the array’s elements until either two equal elements were found or no more pairs were left. Its worst-case efficiency was in  (n²).

Alternatively, we can sort the array first and then check only its consecutive elements: if the array has equal elements, a pair of them must be next to each other, and vice versa.

ALGORITHM     PresortElementUniqueness(A[0..n − 1])

//Solves the element uniqueness problem by sorting the array first //Input: An array A[0..n − 1] of orderable elements

//Output: Returns “true” if A has no equal elements, “false” otherwise sort the array A

for i ← 0 to n − 2 do

if A[i] = A[i + 1] return false return true

The running time of this algorithm is the sum of the time spent on sorting and the time spent on checking consecutive elements. Since the former requires at least n log n comparisons and the latter needs no more than n − 1 comparisons, it is the sorting part that will determine the overall efficiency of the algorithm. So, if we use a quadratic sorting algorithm here, the entire algorithm will not be more efficient than the brute-force one. But if we use a good sorting algorithm, such as mergesort, with worst-case efficiency in  ѳ(n log n), the worst-case efficiency of the entire presorting-based algorithm will be also in  ѳ(n log n):

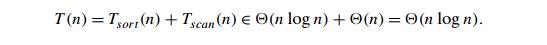
EXAMPLE 2 Computing a mode A mode is a value that occurs most often in a given list of numbers. For example, for 5, 1, 5, 7, 6, 5, 7, the mode is 5. (If several different values occur most often, any of them can be considered a mode.) The brute-force approach to computing a mode would scan the list and compute the frequencies of all its distinct values, then find the value with the largest frequency.

In order to implement this idea, we can store the values already encountered, along with their frequencies, in a separate list. On each iteration, the ith element of the original list is compared with the values already encountered by traversing this auxiliary list. If a matching value is found, its frequency is incremented; otherwise, the current element is added to the list of distinct values seen so far with a frequency of 1.

It is not difficult to see that the worst-case input for this algorithm is a list with no equal elements. For such a list, its ith element is compared with i − 1 elements of the auxiliary list of distinct values seen so far before being added to the list with a frequency of 1. As a result, the worst-case number of comparisons made by this algorithm in creating the frequency list is

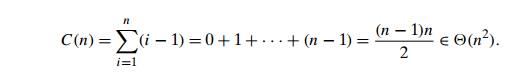
The additional n − 1 comparisons needed to find the largest frequency in the aux-iliary list do not change the quadratic worst-case efficiency class of the algorithm.

As an alternative, let us first sort the input. Then all equal values will be adjacent to each other. To compute the mode, all we need to do is to find the longest run of adjacent equal values in the sorted array.

ALGORITHM                 PresortMode(A[0..n − 1])

//Computes the mode of an array by sorting it first //Input: An array A[0..n − 1] of orderable elements //Output: The array’s mode

sort the array A i ← 0

modef requency ← 0 while i ≤ n − 1 do

runlengt h ← 1;                        runvalue ← A[i]

while i + runlengt h ≤ n − 1 and A[i + runlengt h] = runvalue runlengt h ← runlengt h + 1

if runlengt h > modef requency

modefrequency ← runlengt h; modevalue ← runvalue i ← i + runlengt h

return modevalue

The analysis here is similar to the analysis of Example 1: the running time of the algorithm will be dominated by the time spent on sorting since the remainder of the algorithm takes linear time (why?). Consequently, with an n log n sort, this method’s worst-case efficiency will be in a better asymptotic class than the worst-case efficiency of the brute-force algorithm.

EXAMPLE 3 Searching problem Consider the problem of searching for a given value v in a given array of n sortable items. The brute-force solution here is sequential search (Section 3.1), which needs n comparisons in the worst case. If the array is sorted first, we can then apply binary search, which requires only log₂ n + 1 comparisons in the worst case. Assuming the most efficient n log n sort, the total running time of such a searching algorithm in the worst case will be

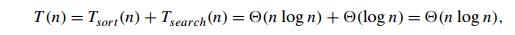
which is inferior to sequential search. The same will also be true for the average-case efficiency. Of course, if we are to search in the same list more than once, the time spent on sorting might well be justified. (Problem 4 in this section’s exercises asks to estimate the minimum number of searches needed to justify presorting.)

Before we finish our discussion of presorting, we should mention that many, if not most, geometric algorithms dealing with sets of points use presorting in one way or another. Points can be sorted by one of their coordinates, or by their distance from a particular line, or by some angle, and so on. For example, presorting was used in the divide-and-conquer algorithms for the closest-pair problem and for the convex-hull problem, which were discussed in Section 5.5.

Further, some problems for directed acyclic graphs can be solved more easily after topologically sorting the digraph in question. The problems of finding the longest and shortest paths in such digraphs (see the exercises for Sections 8.1 and 9.3) illustrate this point.

Finally, most algorithms based on the greedy technique, which is the subject of Chapter 9, require presorting of their inputs as an intrinsic part of their operations.

Exercises 6.1

            Consider the problem of finding the distance between the two closest numbers in an array of n numbers. (The distance between two numbers x and y is computed as |x − y|.)

            Design a presorting-based algorithm for solving this problem and deter-mine its efficiency class.

            Compare the efficiency of this algorithm with that of the brute-force algo-rithm (see Problem 9 in Exercises 1.2).

            Let A = {a₁, . . . , a_n} and B = {b₁, . . . , b_m} be two sets of numbers. Consider the problem of finding their intersection, i.e., the set C of all the numbers that are in both A and B.

            Design a brute-force algorithm for solving this problem and determine its efficiency class.

Design a presorting-based algorithm for solving this problem and deter-mine its efficiency class.

            Consider the problem of finding the smallest and largest elements in an array of n numbers.

            Design a presorting-based algorithm for solving this problem and deter-mine its efficiency class.

            Compare the efficiency of the three algorithms: (i) the brute-force algo-rithm, (ii) this presorting-based algorithm, and (iii) the divide-and-conquer algorithm (see Problem 2 in Exercises 5.1).

            Estimate how many searches will be needed to justify time spent on presorting an array of 10³ elements if sorting is done by mergesort and searching is done by binary search. (You may assume that all searches are for elements known to be in the array.) What about an array of 10⁶ elements?

            To sort or not to sort? Design a reasonably efficient algorithm for solving each of the following problems and determine its efficiency class.

            You are given n telephone bills and m checks sent to pay the bills (n ≥ m). Assuming that telephone numbers are written on the checks, find out who failed to pay. (For simplicity, you may also assume that only one check is written for a particular bill and that it covers the bill in full.)

            You have a file of n student records indicating each student’s number, name, home address, and date of birth. Find out the number of students from each of the 50 U.S. states.

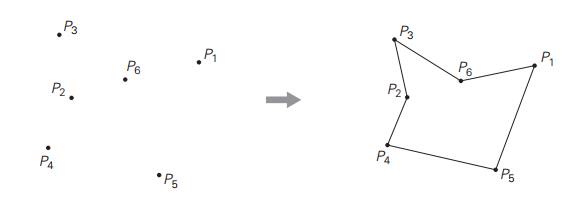
Given a set of n ≥ 3 points in the Cartesian plane, connect them in a simple polygon, i.e., a closed path through all the points so that its line segments (the polygon’s edges) do not intersect (except for neighboring edges at their common vertex). For example,

            Does the problem always have a solution? Does it always have a unique solution?

            Design a reasonably efficient algorithm for solving this problem and indi-cate its efficiency class.

You have an array of n real numbers and another integer s. Find out whether the array contains two elements whose sum is s. (For example, for the array 5, 9, 1, 3 and s = 6, the answer is yes, but for the same array and s = 7, the answer is no.) Design an algorithm for this problem with a better than quadratic time efficiency.

            You have a list of n open intervals (a₁, b₁), (a₂, b₂), . . . , (a_n, b_n) on the real line. (An open interval (a, b) comprises all the points strictly between its endpoints a and b, i.e., (a, b) = {x| a < x < b}.) Find the maximum number of these intervals that have a common point. For example, for the intervals (1, 4), (0, 3), (−1.5, 2), (3.6, 5), this maximum number is 3. Design an algorithm for this problem with a better than quadratic time efficiency.

Number placement Given a list of n distinct integers and a sequence of n boxes with pre-set inequality signs inserted between them, design an algo-rithm that places the numbers into the boxes to satisfy those inequalities. For example, the numbers 4, 6, 3, 1, 8 can be placed in the five boxes as shown below:

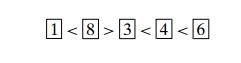
            Maxima search

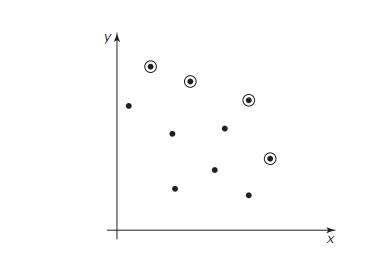
A point (x_i, y_i) in the Cartesian plane is said to be dominated by point (x_j , y_j ) if x_i ≤ x_j and y_i ≤ y_j with at least one of the two inequalities being strict. Given a set of n points, one of them is said to be a maximum of the set if it is not dominated by any other point in the set. For example, in the figure below, all the maximum points of the set of 10 points are circled.

Design an efficient algorithm for finding all the maximum points of a given set of n points in the Cartesian plane. What is the time efficiency class of your algorithm?

b. Give a few real-world applications of this algorithm.

11. Anagram detection

            Design an efficient algorithm for finding all sets of anagrams in a large file such as a dictionary of English words [Ben00]. For example, eat, ate, and tea belong to one such set.

            Write a program implementing the algorithm.