Chapter: Artificial Intelligence(AI) : Planning and Machine Learning
Probability and Bayes’ Theorem
Probability and Bayes’ Theorem
In
probability theory, Bayes' theorem
relates the
conditional and marginal probabilities of two random events.
Probability : The Probabilities are numeric values between 0 and 1 (both inclusive)
that represent ideal uncertainties (not beliefs).
‚ñÝ Probability of event A is P(A)

P(A) = 0 indicates total uncertainty in A,
P(A) = 1 indicates total certainty and
0< P(A) < 1 values in between tells degree of uncertainty
Probability Rules :
All probabilities are between 0 and 1 inclusive 0 <= P(E) <= 1.
The sum of all the probabilities in
the sample space is 1.
The probability of an event which
must occur is 1.
The probability of the sample space
is 1.
The probability of any event which
is not in the sample space is zero.
The probability of an event not
occurring is P(E') = 1 - P(E)
Example 1 : A single 6-sided die is rolled.
What is the probability of each
outcome?
What is the probability of rolling
an even number?
What is the probability of
rolling an odd number?
The possible outcomes of this
experiment are 1, 2, 3, 4, 5, 6.
The Probabilities are :
P(1) = No of ways to roll 1
/ total no of sides = 1/6
P(2) = No of ways to roll 2
/ total no of sides = 1/6
P(3) = No of ways to roll 3
/ total no of sides = 1/6
P(4) = No of ways to roll 4
/ total no of sides = 1/6
P(5) = No of ways to roll 5
/ total no of sides = 1/6
P(6) = No of ways to roll 6
/ total no of sides = 1/6
P(even) = ways to roll even
no / total no of sides = 3/6 = 1/2
P(odd) = ways to roll
odd no / total no of sides = 3/6 = ¬Ω
Example 2 : Roll two dices
Each dice shows one of 6 possible
numbers;
Total unique rolls is 6 x 6 = 36;
List of the joint possibilities
for the two dices are:

Roll two dices;
The rolls that add up to 4 are
((1,3), (2,2), (3,1)).
The probability of rolling dices
such that total of 4 is 3/36 = 1/12 and
the chance of it being true is (1/12) x 100 = 8.3%.
‚ñÝ Conditional probability
P(A|B)
A conditional probability is the
probability of an event given that another event has occurred.
Example : Roll two dices.
What is the probability that the
total of two dice will be greater than 8 given that the first die is a 6 ?
First List of the joint
possibilities for the two dices are:

There are 6 outcomes for which the first die is a 6, and of these,
there are 4 outcomes that total more than 8 are (6,3; 6,4; 6,5; 6,6).
The probability of a total > 8 given that first die is 6 is
therefore 4/6 = 2/3 .

Read as "The probability that
the total is > 8 given that die one is 6 is 2/3."
Written as P(A|B) , is the
probability of event A given that the event B has occurred.
‚ñÝ Probability of A
and B is P(A and B)
The probability
that events A and B both occur.
Note : Two events are independent
if the occurrence of one is unrelated to the probability of the occurrence of
the other.
‡ If A and B are independent
then probability that events A and B both occur is:
P(A and B) = P(A) x P(B)
ie product of probability of A and probability of B.
‡ If A and B are not independent
then probability that events A and B both occur is:
P(A and B) = P(A) x P(B|A) where
P(B|A) is conditional probability of B given A
Example 1: P(A and B) if events A and B are independent
Draw a card from a deck , then
replace it, draw another card. Find probability that 1st card is Ace of clubs
(event A) and 2nd card is any Club (event B).
Since there is only one Ace of
Clubs, therefore probability P(A) = 1/52.
Since there are 13 Clubs, the
probability P(B) = 13/52 = 1/4.
Therefore, P(A and B) = p(A) x p(B)
= 1/52 x 1/4 = 1/208.
Example 2: P(A and B) if events A and B are not independent
Draw a card from a deck, not
replacing it, draw another card. Find probability that both cards are Aces ie
the 1st card is Ace (event A) and the 2nd card is also Ace (event B).
Since 4 of 52 cards are Aces, therefore probability P(A) = 4/52 = 1/13.
Of the 51 remaining cards, 3 are
aces. so, probability of 2nd

‚ñÝ Probability of A or B is P(A or B)
The probability of either event A or event B occur.
Two events are mutually exclusive if they cannot occur at same
time.
‡ If A and B are mutually exclusive
then probability that events A or B occur is:
P(A or B) = p(A) + p(B)
ie sum of probability of A and
probability of B
‡ If A and B are not mutually
exclusive then probability that events A and B both occur is:
P(A or B) = P(A) x P(B|A) – P(A and B) where
P(A and B) is probability that events A and B both occur while events A and B are independent and P(B|A) is conditional probability of B given A.
Example 1: P(A or B) if events A or B are mutually exclusive
Rolling a die.
Find probability of getting
either, event A as 1 or event B as 6? Since it is impossible to get both, the
event A as 1 and event B
as 6 in same roll, these two
events are mutually exclusive. The probability P(A) = P(1) = 1/6 and P(B) =
P(6) = 1/6
Hence probability of either event
A or event B is :
P(A or B) = p(A) + p(B) = 1/6 + 1/6 = 1/3
Example 2: P(A or B) if events A or B are not mutually exclusive
Find probability that a card from
a deck will be either an
Ace or a Spade?
probability P(A) is P(Ace) = 4/52 and P(B) is P(spade) = 13/52.
Only way in a single draw to be
Ace and Spade is Ace of
Spade; which is only one, so
probability P(A and B) is
P(Ace and Spade) = 1/52.
Therefore, the probability of
event A or B is :
P(A or B) = P(A) + P(B) – P(A and
B)
= P(ace) + P(spade) - P(Ace and
Spade)
= 4/52 + 13/52 -
1/52 = 16/52 = 4/13
Summary of symbols & notations


Bayes’ Theorem
.
Bayesian view of probability is
related to degree of
belief.
It is a measure of the plausibility
of an event given incomplete knowledge.
Bayes' theorem is also known as Bayes' rule or Bayes' law, or called
Bayesian reasoning.
The probability of an event A
conditional on another event B ie P(A|B) is generally different from
probability of B conditional on A ie P(B|A).
There is a definite relationship
between the two, P(A|B) and P(B|A), and Bayes' theorem is the statement of that
relationship.
Bayes theorem is a way to calculate
P(A|B) from a knowledge of P(B|A).
Bayes' Theorem is a result that
allows new information to be used to update the conditional probability of an
event.
Bayes' Theorem
Let
S be a sample space.
Let
A1, A2, ... , An be a set of mutually exclusive events from S.
Let B be any event from the same S, such that P(B) > 0. Then Bayes' Theorem describes
following two probabilities :

by invoking the fact P(Ak
‚à©
B) = P(Ak).P(B|Ak) the probability

Applying Bayes' Theorem :
Bayes' theorem is applied while
following conditions exist.
the sample space S
is partitioned into a set of mutually exclusive events {A1, A2, . . . . . , An }.
within S, there exists an event B, for which P(B) > 0.
the goal is to compute a
conditional probability of the form :
P(Ak|B).
you know at least one of the two
sets of probabilities described below
P(Ak ‚à© B) for each Ak
P(Ak) and P(B|Ak) for each Ak
The Bayes' theorem is best
understood through an example below.
Example 1: Applying Bayes' Theorem
Problem : Marie's marriage is tomorrow.
in recent years, each year it has
rained only 5 days. the weatherman has predicted rain for tomorrow.
when it actually rains, the
weatherman correctly forecasts rain 90% of the time.
when it doesn't rain, the
weatherman incorrectly forecasts rain 10% of the time.
The question : What is the
probability that it will rain on the day of Marie's wedding?
Solution : The sample space is
defined by two mutually exclusive events
"it rains" or "it
does not rain". Additionally, a third event occurs when the
"weatherman predicts rain".
The events and probabilities are
stated below.
Event A1 : rains on Marie's wedding.
Event A2 : does not rain on Marie's wedding
Event B : weatherman predicts rain.
P(A1)= 5/365 =0.0136985 [Rains 5
days in a year.]
P(A2)= 360/365 = 0.9863014 [Does
not rain 360 days in a year.]
P(B|A1)= 0.9 [When it rains, the
weatherman predicts rain 90% time.]
P(B|A2)= 0.1 [When it does not
rain, weatherman predicts rain 10% time.]
We want to know P(A1|B),
the probability that it will rain on the day of Marie's wedding, given a
forecast for rain by the weatherman.
The answer can be determined from
Bayes' theorem, shown below.
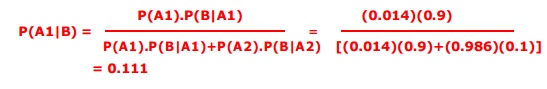
So, despite the weatherman's
prediction, there is a good chance that Marie will not get rain on at her
wedding.
Thus Bayes theorem is used to calculate conditional probabilities.
Example 2: Applying Bayes' Theorem
‡ Let S be a sample space.
‡ Let E1
and E2
be two mutually exclusive events forming a partition
of the sample space S
‚Ä° Let E be any event of the sample space such that P(E) ‚âÝ 0.
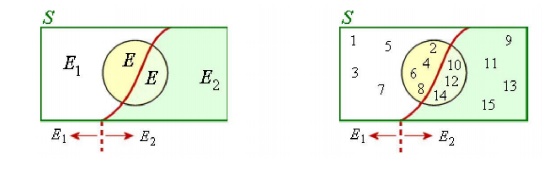
Recall from Conditional Probability
The notation P(E1 | E) means "the probability of the
event E1
given that E has already occurred".
‡ The sample space S
is described as "the integers 1 to 15" and is partitioned into :
E1 = "the integers 1 to 8" and
E2 = "the integers 9 to 15".
‡ If E is the event "even
number" then the probabilities for the situation described by Baye's
Theorem can be calculated in two ways, both giving same results.

Example 3 : Clinic Trial
In a clinic, the probability of the
patients having HIV virus is 0.15.
A blood test done on patients :
If patient has virus, then the test is +ve with probability 0.95.
If the patient does not have the
virus, then the test is +ve with probability 0.02.
Assign labels to events :
Given :
Find :
If the test is +ve
what are the probabilities that the patient
i) has the virus ie P(H|P) ; ii) does not have virus ie P(¬H|P)
;
If the test is -ve what are the probabilities that the patient
iii) has the virus ie P(H|¬P) ; iv) does not have virus ie P(¬H|¬P)
;
Calculations :
For P(H|P) we can write down Bayes Theorem as
P(H|P) = [ P(P|H) P(H) ] / P(P)
We know P(P|H) and P(H) but not P(P)
which is probability of a +ve result. There are two cases, that
a patient could have a +ve result, stated below :
Patient has virus and gets a +ve
result : H
‚à©
P
Patient does not have virus and
gets a +ve result: ¬H ∩ P Find probabilities for the above two cases and then add
ie
P(P) = P(H ∩ P) + P(¬H ∩ P).
But from the second axiom of
probability we have :
P(H ‚à© P) = P(P|H) P(H) and
P(¬H ∩ P) = P(P|¬H) P(¬H).
Therefore putting these we get :
P(P) = P(P|H) P(H) + P(P|¬H) P(¬H) = 0.95 × 0.15 + 0.02 × 0.85 =
0.1595
Now substitute this into Bayes
Theorem and obtain P(H|P)

Related Topics